FUNCTII MATEMATICE UZUALE (I)

FUNCTII MATEMATICE UZUALE (I)

1. GENERAREA VECTORILOR SI A MATRICELOR UZUALE

Functiile folosite pentru generarea vectorilor si a matricelor uzuale sunt:

zeros - Genereaza matricea nula;

ones - Genereaza matricea unitate

eye - Genereaza matricea identica

linspace - Genereaza un vector cu pas liniar;

logspace - Genereaza un vector cu pas logaritmic;

: - Genereaza un vector cu pas constant;

1.1. Generarea vectorilor

1.1.1. Generarea vectorilor cu pas liniar

Generarea vectorilor cu pas liniar implica cunoasterea limitelor intervalului (amin si amax) si a pasului dintre doua elemente (pas) sau a numarului de elemente ale vectorului. Metoda de generare a vectorului se alege in functie de datele de intrare.

Daca se cunosc limitele intervalului (amin si amax) si pasul (pas) dintre doua elemente, se genereaza vectorul cu instructiunea:

x=amin : pas : amax

unde: amin, amax si pas sunt scalari si pot avea orice valoare reala. Numarul de elemente ale vectorului rezultat x este:

unde "[]" semnifica partea intreaga a rezultatului expresiei dintre paranteze. Instructiunea presupune ca:

- daca pas >0, atunci este necesar ca amin < amax;

- daca pas < 0, atunci este necesar ca amin >amax.

Spre exemplu:

x=2:5:25

x=-20:3:10

x=5:-2:-4

x=-15:-3:-25

x=5:15

sunt corecte, in timp ce urmatoarele instructiuni:

x=2:-1:5

x=-5:2:-10

sunt incorecte.

Daca pasul se omite, valoarea acestuia este considerata implicit egala cu unitatea.

Daca se cunosc limitele intervalului (amin si amax) si numarul de elemente (N) ale vectorului generat cu pas liniar, atunci se foloseste instructiunea:

x=linspace(amin, amax, N)

Pasul dintre doua elemente rezulta egal cu:

Daca valoarea N este omisa, atunci aceasta este considerata implicit egala cu 100. Valorile limitelor intervalului, amin si amax, nu sunt supuse nici unei restrictii si pot fi date in orice ordine, (daca amin >amax vectorul generat va fi ordonat descrescator).

Exemplul1. Sa se genereze un vector cu pas liniar, cu limitele: amin=2.5, amax=7 si pasul egal cu 1.25. Secventa:

x= 2.5 : 1.25 : 7

conduce la rezultatul:

x=[2.5000 3.7500 5.0000 6.2500]

Exemplul 2. Sa se genereze un vector cu pas liniar, cu limitele: amin = 2.5, amax = 7 si N = 4 elemente. Secventa:

x=linspace(2.5 ,7, 4)

conduce la rezultatul:

x=[2.5000 4.0000 5.5000 7.0000]

Desi genereaza acelasi numar de elemente, prima secventa controleaza pasul si poate modifica eventual limita superioara, iar a doua controleaza numarul de elemente si mentine limitele impuse.

1.1.2. Generarea vectorilor cu pas logaritmic

Functia logspace genereaza vectori cu pas logaritmic; se apeleaza cu sintaxa:

x=logspace(amin, amax, N)

Vectorul x contine N elemente distribuite logaritmic intre decadele . Daca numarul de elemente N este omis, se genereaza un vector cu 50 de elemente distribuite logaritmic intre decadele . Daca , elementele vectorului sunt distribuite intre si . Valorile limitelor intervalului, amin si amax, nu au nici o restrictie si pot fi date in orice ordine. Daca amin>amax, vectorul generat va fi ordonat descrescator.

Exemplul 1. Sa se genereze un vector cu N=5 elemente distribuite logaritmic pe intervalul [10^-2, 10²]. Secventa:

x=logspace (-2, 2, 5)

determina rezultatul:

x=[0.0100 0.1000 1.0000 10.0000 100.0000]

Exemplul 2. Sa se genereze un vector cu N=6 elemente distribuite logaritmic pe intervalul [10^-2, p]. Secventa:

x=logspace (-2, pi, 6)

determina rezultatul:

x=[0.0100 0.0316 0.0997 0.3150 0.9948 3.1416]

1.2. Generarea matricelor

1.2.1. Matricea unitate

Matricea unitate este o matrice cu toate elementele 1:

si poate fi generata cu functia ones; se apeleaza cu una dintre sintaxele:

U=ones(n) U=ones(m,n) U=ones(size(A))

Unde m si n sunt scalari, iar A este matrice. Daca functia ones este apelata cu un singur argument scalar, matricea generata este o matrice patrata, avand dimensiunea argumentului. Apelata cu doua argumente scalare (m,n), matricea generata are m linii si n coloane. Daca functia ones are ca argument o matrice A, matricea generata este o matrice unitate de aceleasi dimensiuni cu matricea A.

Exemplul 1. Sa se genereze o matrice unitate cu dimensiunea 2x2 si o matrice unitate cu dimensiunea 2x3. Cu secventa:

A1=ones(2)

A2=ones(2, 3)

se obtine rezultatul:

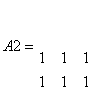
Exemplul 2. Fie matricea .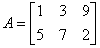

Sa se genereze o matrice unitate de aceleasi dimensiuni cu matricea A.

Cu secventa:

A=[1 3 9; 5 7 2];

U=ones(size(A))

se obtine rezultatul:

1.2.2. Matricea zero

Matricea zero este o matrice cu toate elementele zero:

si poate fi generata cu functia zeros, care se apeleaza cu una dintre sintaxele:

O=zeros(n) O=zeros(m,n) O=zeros(size(A))

unde m si n sunt scalari, iar A este matrice. Daca functia zeros este apelata cu un singur argument scalar, matricea generata este o matrice patrata, avand dimensiunea argumentului. Apelata cu doua argumente scalare (m,n), matricea generata are m linii si n coloane. Daca functia zeros are ca argument o matrice A, matricea generata este o matrice unitate de aceleasi dimensiuni cu matricea A.

1.2.3. Matricea identitate

Matricea identitate este o matrice care are elementele de pe diagonala principala egale cu unu, iar toate celelalte elemente egale cu zero.

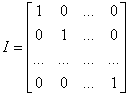
Se genereaza cu functia eye, care se apeleaza cu una din sintaxele:

I=eye(n) I=eye(m,n) I=eye(size(A))

unde m si n sunt scalari, iar A este matrice. Daca functia eye este apelata cu un singur argument scalar, matricea generata este o matrice patrata, avand dimensiunea argumentului. Apelata cu doua argumente scalare (m,n), matricea generata are m linii si n coloane. Daca functia zeros are ca argument o matrice A, matricea generata este o matrice unitate de aceleasi dimensiuni cu matricea A.

Exemplul 1. Sa se genereze o matrice identitate cu dimensiunea 2x2 si o matrice identitate cu dimensiunea 2x3. Cu secventa:

A1=eye(2)

A2=eye(2, 3)

se obtine rezultatul:

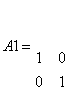
Exemplul 2. Fie matricea .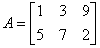

Sa se genereze o matrice identitate de aceleasi dimensiuni cu matricea A.

Cu secventa:

A=[1 3 9; 5 7 2];

I=eye(size(A))

se obtine rezultatul:

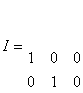
2. APROXIMAREA NUMERELOR

Functiile MATLAB folosite pentru aproximarea numerelor sunt:

ceil - Returneza un numar intreg, rotunjit la cel mai apropiat intreg spre plus infinit (+¥

fix - Returneaza un numar intreg, rotunjit la cel mai apropiat intreg spre zero;

floor - Returneaza un numar intreg, rotunjit la cel mai apropiat intreg spre minus infinit (-¥

round - Returneaza un numar intreg, rotunjit la cel mai apropiat intreg;

rem - Returneaza restul impartirii argumentelor;

rat - Returneaza aproximarea unui numar cu fractii rationale continue;

rats - Returneaza aproximarea unui numar cu numere rationale;

sign - Returneaza semnul argumentului.

2.1. Aproximarea cu numere intregi

Functiile MATLAB folosite pentru aproximarea cu numere intregi sunt: fix, floor, ceil, round. Aceste functii opereaza asupra fiecarui element al unei matrice sau al unui vector si se apeleaza cu sintaxa:

nume_functie(argument)

unde:

- nume_functie este numele uneia dintre functiile de mai sus;

- argument poate fi un scalar, un vector sau o matrice, ale caror elemente se doresc a fi rotunjite.

Daca elementele din argumetul functiei sunt numere complexe, functiile de mai sus opereaza independent asupra fiecarei parti (reala si imaginara).

Exemplul 1. Sa se rotunjeasca elementele vectorului:

V=[0 2 2.3 4.7 -5.2 -7.8]

- la cel mai apropiat intreg;

- la cel mai apropiat intreg spre zero;

- la cel mai apropiat intreg spre +¥

- la cel mai apropiat intreg spre -¥

Sa se determine semnul elementelor vectorului V.

Cu secventa de instructiuni:

V=[0 2 2.3 4.7 -5.2 -7.8]

A=round(V)

B=fix(V)

C=ceil (V)

D=floor(V)

E=sign(V)

se obtin rezultatele:

A=[0 2 2 5 -5 -8]

B=[0 2 2 4 -5 -7]

C=[0 2 3 5 -5 -7]

D=[0 2 2 4 -6 -8]

E=[0 1 1 1 -1 -1]

Exemplul 2. Acelasi enunt ca mai sus, pentru o matrice cu elemente numere complexe:

Cu secventa de instructiuni:

W=[1.25+2.59*i 7.3-5.3*i;

-4.2+1.8*i -2.6-1.4*i]

A=round(W)

B=fix(W)

C=ceil(W)

D=floor(W)

E=sign(W)

se obtin rezultatele:

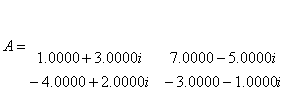
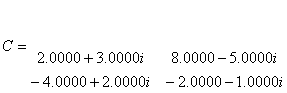
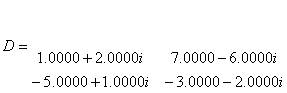
2.2. APROXIMAREA CU NUMERE RATIONALE

Functia MATLAB rats realizeaza aproximarea cu numere rationale; se apeleaza cu una dintre sintaxele:

y=rats(x) y=rats(x,^/s^/)

Argumentul de intrare ^/s^/ determina afisarea rezultatului simbolic y intr-o matrice sir.

Exemplu. Sa se aproximeze cu numere rationale, numerele: 1.25, 0.25, p si 1.2596.

Cu secventa:

X=[1.25 0.25 pi 1.2596];

Y=rats(X)

se obtin rezultatele:

Y=[5/4 1/4 355/113 820/651]

2.3. APROXIMAREA CU FRACTII CONTINUE

Functia MATLAB rat aproximeaza un numar cu fractii continue; se apeleaza cu una dintre sintaxele:

y=rat(x) [a, b]=rat(x)

y=rat(x, tol) [a, b]=rat(x, tol)

unde:

x - este numarul care trebuie aproximat cu fractii continue;

tol - este toleranta care se accepta intre numarul x si numarul y (y-x<=tol); implicit, tol=10^-6;

y - exprimarea lui x ca ftactie continua;

a si b - numaratorul si numitorul fractiei care aproximeaza pe x cu toleranta tol.

Functia rat aproximeaza fiecare element al vectorului x cu un numar de forma:

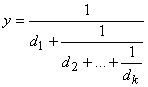
Exemplul 1. Sa se aproximeze cu fractii continue numerele: 0.25, 1.25, -2.25 si 1.343.

Cu secventa MATLAB:

rat([0.25 1.25 -2.25 1.343])

se obtine rezultatul:

0+1/(4)

1+1/(4)

-2+1/(-4)

1+1/(3+1/(-12+1/(6)))

Solutia corespunde urmatoarelor descompuneri in fractii continue:

Exemplul 2. Sa se aproximeze prin fractii rationale numerele: 2.25, 3.5, 6.57, 10. Se inscriu aceste numere intr-un vector si se aplica functia rat, ca in secventa de mai jos:

X=[2.25 3.5 6.57 10]

[A, B]=rat(X)

obtinandu-se rezultatul:

X=[2.25 3.5 6.57 10]

A=[9 7 657 10]

B=[4 2 100 1]

Adica o aproximare a numerelor date, prin urmatoarele fractii:

2.25=9/4 3.5=7/2

6.57=657/100 10=10/1

2.4. FUNCTIA REST

Functia rem(X, Y) calculeaza restul impartirii lui X la Y, element cu element. Dacaelementele vectorului sau matricei sunt numere complexe, partea imaginara este ignorata. Argumentele X si Y trebuie sa fie matrice de aceeasi dimensiune, sau unul dintre ele sa fie scalar.

Exemplul 1. Sa se calculeze restul impartirii elementelor vectorului X la Y.

Cu secventa:

X=[1 3 -6]

Y=[2 3 4]

Z=rem(X, Y)

se obtine rezultatul

Z=[1 0 -2]

Exemplul 2. Sa se determine restul impartirii unui vector la un scalar si al unui scalar la un vector.

Cu secventa MATLAB:

X=[2.5 6 -7]

Y=3

Z1=rem(X,Y)

se obtin rezultatele:

Z1=[2.5000 0 -1.0000]

Z2=[0.5000 3.0000 3.0000]

Exemplul 3. Fie vectorii:

X=[1 i -6+2i]

Y=[2+i 3+2i 3-i]

Sa se calculeze restul impartirii elementelor complexe ale vectorului X la Y.

Cu secventa de instructiuni:

X=[1 I -6+2*i]

Y=[2+i 3+2*i 3-i]

Z=rem(X/Y)

se obtine rezultatul:

Z=[1 0 0]

2.5. FUNCTIA SEMN

Functia sign asociaza fiecarui element al vectorului X elementele -1, 0, 1, dupa urmatoarea regula:

1, daca X > 0;

sign(X) = 0, daca X = 0;

-1, daca X < 0

3. DIVIZORI ÈI MULTIPLI COMUNI

Pentru calculul divizorilor si al multiplilor comuni se folosesc functiile:

gcd - Calculeaza cel mai mare divizor comun a doua numere;

lcm - Calculeaza cel mai mic multiplu comun a doua numere.

3.1. Cel mai mare divizor comun

Functia MATLAB gcd calculeaza cel mai mare divizor comun a doua numere intregi; se apeleaza cu sintaxa:

a=gcd(x, y)

Exemplu. Sa se determine cel mai mare divizor comun al numerelor 30 si 21.

Cu secventa:

a=gcd(30, 21)

rezulta:

a=3.

3.2. Cel mai mic multiplu comun

Functia MATLAB lcm returneaza cel mai mic multiplu comun a doua numere intregi; se apeleaza cu sintaxa:

a=lcm(x, y)

Exemplu. Sa se determine cel mai mic multiplu comun al numerelor 9 si 30.

Cu secventa:

a=lcm(9, 30)

rezulta:

a=90

4. PROBLEME PROPUSE

1. Sa se rotunjeasca elementele vectorului V=[0 3 3.3 5.8 -4.2 -8.9] la cel mai apropiat intreg spre plus infinit.

2. Sa se determine c.m.m.d.c. al numerelor 40, 60. Sa se determine c.m.m.m.c. al numerelor 6, 90.

3. Sa se determine restul impartirii elementelor vectorului X la vectorul Y, unde:

X = [2 5 6 12]; Y = [3 7 8 10].

4. Sa se rotunjeasca elementele vectorului V=[1 4 7.3 7.8 -3.3 7.4] la cel mai apropiat intreg spre minus infinit.

5. Sa se determine c.m.m.d.c. al numerelor 20, 80. Sa se determine c.m.m.m.c. al numerelor 8, 40.

6. Sa se determine restul impartirii elementelor vectorului X la vectorul Y, unde:

X = [1 2 8 11]; Y = [3 5 2 14].

7. Sa se determine c.m.m.d.c. al numerelor 35, 85. Sa se determine c.m.m.m.c. al numerelor 8, 120.

8. Sa se rotunjeasca elementele vectorului V=[1 2 5.7 7.2 -2.8 -7.9] la cel mai apropiat intreg spre plus infinit.

9. Sa se determine c.m.m.d.c. al numerelor 40, 60. Sa se determine c.m.m.m.c. al numerelor 6, 90.