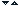Criterii de convergenta

Criterii de convergenta

Teorema (Criteriul necesar de convergenta) Fie o serie de numere reale. Daca este convergenta atunci .

Demonstratie:Fie Atunci a_n= s_n - s_n-1.

Cum este convergenta rezulta ca exista si deci

Exemplu Sa se studieze natura seriei:

2)

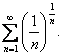
Solutie: 1) si din Criteriul de convergenta se obtine ca seria este divergenta.

2)

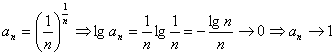
Din Criteriul necesar de convergenta rezulta ca seria este divergenta.

Observatie Reciproca este falsa.

Exemplu Sa se arate ca seria este divergenta desi

Solutie: Pentru a justifica ca seria este divergenta observam ca sirul sumelor partiale este:

care tinde spre infinit apoi termenul seriei tinde spre 0 dupa cum rezulta din

Teorema (Criteriul general al lui Cauchy) Fie o serie de numere reale . este convergenta daca si numai daca astfel incat:

.

Demonstratie: Sirul sumelor partiale (s_n) este convergent daca si numai daca este sir Cauchy, adica:

Exemplu Sa se studieze natura seriei:

Solutie:

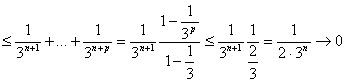
Din criteriul general al lui Cauchy va rezulta ca seria este convergenta.

Teorema Fie o serie cu termeni pozitivi. este convergenta daca si numai daca sirul sumelor partiale (s_n) este marginit.

Demonstratie: Daca este convergenta rezulta ca (s_n) este convergent si deci el este marginit.

Reciproc , cum s_n+1-s_n= a_n+1, avem ca (s_n) este monoton si cum el este marginit din ipoteza el va fi convergent, deci este convergenta.

Teorema (Criteriul de condensare) Daca este un sir monoton descrescator de numere pozitive atunci este convergenta daca si numai daca este convergenta.

Demonstratie: Ambele sunt serii cu termeni pozitivi. In baza teoremei precedente convergenta lor este echivalenta cu marginirea sirurilor sumelor partiale. Fie:

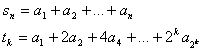
Aceste siruri.

Pentru k dat alegem n astfel incat . Atunci:

Cum (t_k) este marginit rezulta (s_n) este marginit.

Corolar:Seria armonica generalizata este convergenta daca si numai daca p>1.

Demonstratie: Pentru avem si aplicand criteriul necesar de convergenta seria va fi divergenta.

Daca p>0, conform Criteriului de condensare, seria data va avea aceeasi natura cu seria:

care este seria geometrica si este convergenta daca si

numai daca 2^1-p <1 adica p>1.

Exemplu Sa se studieze natura seriei:

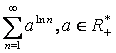
Solutie: Sa observam ca termenul seriei este

si deci seria data este chiar seria armonica generalizata si va fi convergenta daca si numai daca

>1.

Teorema (Criteriul I al comparatiei) Fie doua serii cu termeni pozitivi. Presupunem ca exista astfel incat Atunci:

1. convergenta este convergenta;

2. este divergenta este divergenta.

Demonstratie: 1.Putem presupune ca (Neglijand primii N termeni din ambele serii nu se modifica natura acestora) Daca convergenta rezulta ca sirul sumelor partiale ale acestei serii este marginit si cum vom avea ca sirul sumelor partiale ale seriei este marginit, deci aceasta serie este convergenta.

2.Presupunem convergenta. Rezulta, din punctul precedent , ca seria este convergenta, ceea ce este in contradictie cu ipoteza.

Exemplu Sa se studieze natura seriei:

1.

2.

Solutie: 1) pentru n>3. Aplicam Criteriul intai al comparatiei. Cum este seria armonica divergenta (p=1/2<1) rezulta ca seria data este divergenta.

2) pentru Vom aplica criteriul intai al comparatiei, notand ca este seria armonica convergenta (p=2>1) si atunci si seria este convergenta.

Teorema (Criteriul al II-lea al comparatiei) Fiind date seriile ,, , daca exista atunci cele doua serii au aceeasi natura.

Demonstratie: Daca:

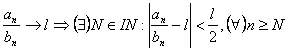
Adica

Daca presupunem ca este convergenta rezulta este convergenta si aplicand Criteriul I al comparatiei, cum , avem ca este convergenta. Daca presupunem ca este divergenta atunci este divergenta si Criteriul I al comparatiei impreuna cu inegalitatea conduc la faptul ca este divergenta , ceea ce incheie demonstratia.

Exemplu Sa se studieze natura seriei

1.;

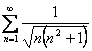2. .

Solutie: 1) Vom aplica Criteriul al doilea al comparatiei si vom compara seria data cu , seria armonica convergenta (p=3/2>1). In acest scop notam ca :

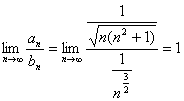
si astfel cele doua serii au aceeasi natura , deci seria data este convergenta.

2) Daca a>1, folosind si ca este seria geometrica convergenta, aplicand Criteriul intai al comparatiei se obtine ca seria data este convergenta.

Daca a =1 seria considerata este chiar seria armonica divergenta.

Pentru a<1 avem

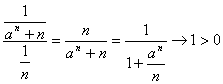
Si din criteriul al doilea al comparatiei, cum este divergenta si seria initiala este divergenta .

Teorema (Criteriul lui Abel) Fie o serie de numere reale avand sirul sumelor partiale marginit. Daca este un sir de numere reale monoton descrescator si convergent la zero atunci este convergenta.

Demonstratie: Fie

Conform ipotezei Atunci:

Fie acum Cum rezulta ca :

Revenind obtinem:

.

Criteriul general al lui Cauchy ne spune ca seria este convergenta.

Teorema (Criteriul Leibniz) Daca este un sir de numere reale monoton descrescator si convergent la zero atunci seria alternanta este convergenta.

Demonstratie: Aplicam Criteriul Abel ci a_n = (-1)^n-1, observand ca este 0 pentru n par si 1 pentru n impar, deci este marginit.

Exemplu Sa se studieze natura seriei:

Solutie: Seria este convergenta din Criteriul lui Leibniz, caci este evident un sir monoton descrescator si convergent la zero.

Definitie O serie se numeste absolut convergenta daca seria este convergenta.

Exemplu Sa se studieze natura seriei:

Solutie : 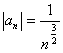si seria armonica este convergenta (p=3/2>1), deci seria data este absolut convergenta.

Teorema Orice serie absolut convergenta este convergenta.

Demonstratie: Daca este convergenta , din Criteriul general al lui Cauchy, avem :

:

. Dar:

Si aplicand inca o data acelasi Criteriu al lui Cauchy rezulta ca este convergenta.

Observatie Reciproca este falsa .

Exemplu Seria este convergenta dar nu este absolut convergenta.

Solutie: Intr-adevar, seria este convergenta din Criteriul lui Leibniz, sirul fiind monoton descrescator si convergent la zero.Seria aleasa nu este absolut convergenta pentru ca seria modulelor este seria armonica care este divergenta.

Teorema (Criteriul radacinii al lui Cauchy) Fie o serie de numere reale.Daca exista atunci :

daca este absolut convergenta;

daca este divergenta.

Demonstratie: 1) Daca l<1 rezulta ca exista p: l < p < 1.Cum obtinem :

Utilizand Criteriul I al comparatiei, comparand cu seria geometrica, se obtine ca seria este convergenta, deci este absolut convergenta.

2) Daca l>1 rezulta ca exista r: l > r >1.In mod analog aceasta va conduce la .Dar si deci a_n nu tinde la zero. Criteriul necesar de convergenta ne spune ca este divergenta.

Exemplu Sa se studieze natura seriei:

1.

2.

Solutie:

Aplicam Criteriul radacinii lui Cauchy:

Daca a<1 seria este convergenta, iar daca a>1 seria este divergenta..

Daca a=1 atunci

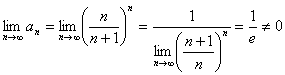
si din Criteriul necesar de convergenta va rezulta ca seria este divergenta.

Vom aplica Criteriul radacinii al lui Cauchy:

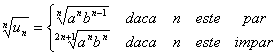
Rezulta ca exista . Atunci daca ab<1 seria este convergenta, iar daca ab>1 seria este divergenta. Daca ab=1 atunci b=1/a si seria devine 1 + a + 1 + a + 1 + a + care este divergenta.