Aproximarea numerica a functiilor in Matlab

Aproximarea numerica a functiilor in Matlab

1. Aspecte generale

Aproximarea functiilor pe cale numerica este utila si necesara si in special in doua cazuri:

• functia care trebuie prelucrata are o expresie analitica dar, aceasta este suficient de complicata incat face dificila manipularea;
• functia nu mai are o expresie analitica cunoscuta, ea fiind data sub forma tabelara prin puncte.

Problema aproximarii unei functii porneste de la functia originala f(x) incercand determinarea unei functii de aproximare F(x).

Exista mai multe metode de rezolvare:

• Aproximarea prin interpolare. In acest caz functia de aproximare se determina impunand conditia ca ea sa coincida cu functia originala in anumite puncte de pe axa numerelor reale.
• Aproximarea folosind curbe spline. In acest caz in afara de coincidenta celor doua functii intr-o serie de puncte de pe axa reala se impune si conditia coincidentei derivatelor functiei originale si de aproximare pana la un anunit ordin.
• Aproximarea dupa metoda celor mai mici patrate. In acest caz functia de aproximare se determina impunand conditia ca suma patratelor distantelor dintre functia originala si cea de aproximare in anumite puncte sa fie minima.

2. Aproximarea functiilor prin interpolare

Se considera o functie originala f(x) definita sub forma tabelara. In acest scop, se considera faptul ca valorile x constituie cele n+1 puncte distincte, cunoscute ale functiei y=f(x) in intervalul [a,b]:

adica:

(x_k , y_k) , y_k = f(x_k) , k = 1, 2, , n+1 (1)

In cazul cel mai general, cele n+1 puncte distincte pot fi oarecare in intervalul [a,b]. In majoritatea cazurilor ele sunt echidistante, cu pasul de discretizare h:

h = x_k+1 - x_k    (2)

primul si ultimul corespunand limitelor intervalului, adica x₁=a, respectiv x_n+1=b.

Criteriul de interpolare determina functia de aproximare F(x) impunand conditia ca acesta sa coincida cu functia originala f(x) in puncte din tabelul de definitie a functiei:

F(x_k) = y_k, k = 1, 2, , n+1 (3)

In functie de forma functiei de interpolare se disting:

• interpolare polinomiala, cand functia F(x) este un polinom;
• interpolare rationala, cand functia F(x) este o fractie simpla sau etajare;
• interpolare logaritmica, exponentiala sau trigonometrica.

2.1. Interpolarea polinomiala

In cazul interpolarii polinomiale functia de aproximare are expresia:

F(x) = a₁ + a₂x + a₃x² + + a_n+1xⁿ    (4)

Cunoasterea polinomului F(x) presunune determinarea coeficientilor a₁, , a_n+1. daca se scrie expresia (4) pentru fiecare k = 1, 2, , n+1, va rezulta un sistem de ecuatii liniar de forma:

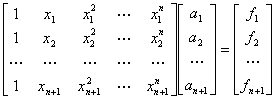    (5)

Sistemul (5) poate fi scris sub forma restransa, astfel:

[V] [A] = [f] → [A] = [V]^-1 [f]    (6)

Daca n este mare, rezolvarea sistemului (5) este dificila sau cel putin neconvenabila. In orice caz, nodurile x_k fiind distincte, sistemul de ecuatii (5) este un sistem cu determinant Vandermonde diferit de zero si are o solutie unica, bine determinata pentru coeficientii a_k. In consecinta, oricare ar fi calea pe care se construieste efectiv polinomul de interpolare (4), acesta este unic pentru o functie si o diviziune data. Aproximarea efectuata este o interpolare globala ın sensul ca se foloseste un singur polinom pe tot intervalul [x₀, x_n].

Modelul matematic de definitie a matricei Vandermonde este dat de relatia:

V(i,j)=x(i)^(n-j)

In Matlab matricea Vandermonde poate fi definita cu ajutorul functiei vander. Sintaxa de apelare a acestei functii este:

V = vander (x),

unde x este un vector cu n elemente ce reprezinta numarul de noduri de interpolare in care functia f(x) este definita, iar V este matricea Vandermonde rezultata.

2.2. Interpolarea cu polinoame Newton pentru un suport de interpolare oarecare

Prin suport de interpolare oarecare se intelege o distributie intamplatoare a nodurilor de interpolare in intervalul de definitie. In cazul polinomului de interpolare Newton, polinomul de aproximare nu mai foloseste distanta la origine ca in cazul relatiei (4) ci distanta fata de nodurile de interpolare. In general in aceste polinoame vor interveni expresii de forma: (x-x₁), (x-x₂), , (x-x_n). Pentru a individualiza metoda, functia de interpolare o vom nota cu N_n(x), unde n reprezinta gradul polinomului.

Pentru deducerea expresiei generale se foloseste notiunea de diferenta divizata. Relatia generala de calcul a unei diferente divizate este urmatoarea:

    (7)

unde j indica ordinul diferentei divizate, iar j indica nodul de interpolare de la care este definita acea diferenta divizata.

In final, expresia generala a functiei de interpolare bazata pe polinomul Newton este urmatoare:

(8)

Din analiza expresiei (8) se constata ca determinarea polinomului Newton necesita cunoasterea tuturor diferentelor divizate in raport cu primul nod de interpolare. Dar, daca se analizeaza si expresia (7) se constata ca pentru a calcula pe δ_1,n+1 este nevoie de toate diferentele divizate. Astfel, utilizarea expresiei (8) pentru aproximare necesita memorarea tuturor diferentelor divizate care pot fi definite pentru suportul de interpolare considerat.

Un alt dezavantaj al utilizarii expresiei (8) il reprezinta faptul ca polinomul de aproximare are un grad impus de numarul de noduri de interpolare care se precizeaza.

Datorita acestor aspecte s-a cautat adaptarea metodei astfel incat polinomul de aproximare sa poata avea orice grad pana la gradul n inclusiv.

Astfel a fost dezvoltat algoritmul modificat al interpolarii cu polinoame Newton. Particularitatea acestuia consta in faptul ca inainte de aproximarea cu polinomul Newotn se procedeaza la o reordonare a nodurilor de interpolare in raport cu punctul x^* in care se doreste aproximarea functiei, x^* < x₁ < x₂ < < x_n+1.

Dupa ce s-a facut reordonarea se procedeaza la aproximarea functiei f(x) succesiv prin polinoame Newton cu grad din ce in ce mai mare. Daca se foloseste ca punct de interpolare x_k, atunci:

(9)

Daca se foloseste un singur nod de interpolare functia este aproximata printr-o constanta. Daca se folosesc doua noduri de interpolare functia este aproximata printr-o dreapta, s.a.m.d.

In practica, de cele mai multe ori se utilizeaza o aproximare printr-un polinom de gradul 3, care multumeste utilizatorul din punct de vedere al erorii.

2.2.1. Interpolarea functiilor in Matlab

In cele ce urmeaza sunt prezentate trei tipuri de interpolari: liniara, spline cubica si polinomiala. In toate cazurile se presupune ca exista un set de date care reprezinta coordonatele (x_k,y_k). Obiectivul il constituie estimarea valorilor functiei f(x), pentru orice punct x_k, k = 1,2,,n+1. Curba de interpolare trece prin toate punctele care o definesc, legea de interpolare intre puncte putand fi liniara, cubica sau polinomiala. Daca punctele sunt unite printr-o dreapta, interpolarea se numeste liniara, iar daca sunt unite printr-un polinom de gradul trei, interpolarea este spline cubica.

Functia Matlab interp1 poate interpola datele dupa o lege liniara, cubica sau spline cubica. Aceasta poate fi apelata cu sintaxa:

F = interp1(x, y, xk, 'regula')

unde regula este unul dintre cuvintele cheie:

• linear - pentru interpolare liniara;
• spline - pentru interpolare spline cubica;
• cubic - pentru interpolare cubica.

Toate legile de interpolare necesita ca x sa fie ordonat monoton. In plus, metoda 'cubic' cere ca toate punctele de pe axa x sa fie egal distantate.

Daca y este o matrice cu numarul de linii, n, egal cu cel al vectorului x si cu N coloane, functia interp1 returneaza o matrice cu un numar de linii egal cu cel al vectorului x_k si cu N coloane.

2.3. Algoritmul de aplicare a metodei Newton

3. Aproximarea folosind metoda celor mai mici patrate

In cazul aproximarii prin interpolare a unei functii f(x) definita tabelar conditia care trebuie respectata (functia de aproximare F(x) trebuie sa coincida cu functia aproximant f(x) in toate nodurile de interpolare) imprima curbei de aproximare o traiectorie impusa de punctele prin care este definita functia. Acest criteriu da rezultate bune atata timp cat nodurile de interpolare prezinta o dispersie relativ mare unele in raport cu altele.

Modelarea matematica a criteriului celor mai mici patrate:

(10)

In relatia (10) S reprezinta functia obiectiv si ea este definita ca fiind suma patratelor abaterilor intre valorile functie original f(x) si de aproximare F(x) in nodurile de interpolare.

Minimizarea functiei S in situatia in care erorile inerente de estimare sunt localizate la nivelul functiei original f(x) poarta denumirea de regresie in x. Daca dimpotriva erorile inerente de estimare se localizeaza in varianta x atunci se vorbeste despre regresia in f sau y.

Dupa forma functiei de aproximare F(X) putem avea:

regresie polinomiala;

regresie exponentiala;

regresie logaritmica, etc.

Dintre aceste forme ale functiei F(x), pentru majoritatea fenomenelor din practica, cea mai potrivita este regresia polinomiala cu un caz particular, regresia liniara.

3.1. Regresia polinomiala

Pentru functia de aproximare aleasa sub forma unui polinom expresia abaterii medii patratice devine:

(11)

Pentru acest tip de regresie functia obiectiv S are forma:

(12)

Exista mai multe metode de minimizare a functiei obiectiv S. Dintre acestea cea mai simpla si utilizata metoda este cea a anularii derivatelor partiale corespunzatoare functiei obiectiv in raport cu necunoscutele problemei. In cazul regresie polinomiale necunoscutele sunt reprezentate de coeficientii a_i, i = 0, p, din expresia functiei de aproximare F(x). Acesti coeficienti trebuie determinati atfel incat sa se asigure determinarea valorii minime pentru functia obiectiv.

In urma anularii derivatelor partiale in raport cu necunoscutele a_i, i = 0, p, si in urma unor calcule repetate se vor obtine necunoscutele si anume coeficientii a_i., prin rezolvarea sistemului de ecuatii liniare.

In cele ce urmeaza este prezentat cazul particular al regresiei polinomiale si anume regresia liniara.

3.2. Regresia liniara

Se presupun cunoscute valorile tabelate f₀, f₁, , f_n ale unei functii, corespunzatoare nodurilor x₀, x₁, , x_n. Se presupune de asemenea ca valorile tabelate pot fi aproximate cu o functie liniara:

(13)

Constantele a₀ si a₁ trebuie astfel determinate incat suma patratelor abaterilor sa fie minima, adica:

(14)

Pentru ca S sa fie minim, trebuie ca derivatele partiale de ordinul intai ale lui S in raport cu necunoscutele a₀ si a₁ sa fie egale cu zero, adica:

(15)

Ordonand termenii, se obtine:

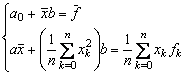(16)

unde

(17)

reprezinta valorile medii ale lui x si f.

Dupa rezolvarea sistemului (23) rezulta:

; (18)

Relatiile (18) sunt sensibile la erorile de rotunjire. Din acest motiv determinarea coeficientilor a₀ si a₁ poate fi facuta cu ajutorul urmatoarelor relatii:

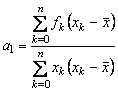; (19)

Solutia (a₀, a₁) exista si este unica atata timp cat sunt tabelate doua sau mai multe valori ale lui x. Inlocuind (a₀, a₁) solutia in ecuatia dreptei, se obtine aproximarea liniara prin metoda celor mai mici patrate.

Functia de aproximare F(x) poate avea si forme neliniare, care pot fi liniarizate pentru a putea fi aplicat criteriul celor mai mici patrate.

4. Mersul lucrarii

Se studiaza textul lucrarii;

Sa se genereze o matrice de tip Vandermonde definita prin vectorul x=[1 2 3 4].

Se da sub forma tabelara urmatoarea functie:

Sa se determine folosind functia Matlab interp1 valoarea functiei de aproximare care corespunde lui x1 = -1 si x2 = 3, folosind interpolarea liniara, cubica si spline cubica.

Se testeaza programul de calcul corespunzator metodei de interpolare cu polinoame de tip Newton.

Se solutioneaza cateva aplicatii numerice semnificative, prezentandu-se rezultatele sub forma grafica.

Se considera o functie reala y = f(x) pentru care se cunosc valorile in 6 puncte echidistante ale intervalului [0, 5], cu pasul de discretizare h = 1.

Sa se reprezinte grafic rezultatele obtinute prin aproximarea functiei f(x) cu polinoame de gradul 1, 3, 5 si 7 obtinute prin metoda celor mai mici patrate.