Mentenabilitatea si mentenanta sistemelor

Mentenabilitatea si mentenanta sistemelor

1. Caracteristici si probleme generale

Mentenabilitatea unui sistem este proprietatea acestuia de a putea fi usor mentinut sau readus (restabilit) in stare de buna functionare, intr-un timp cat mai scurt.

Activitatile legate de mentinerea sau readucerea sistemului in stare de buna functionare, se numesc activitati de mentenanta. Ansamblul lor formeaza mentenanta sistemului.

Activitatile de mentenanta pot fi preventive atunci cand au ca scop prevenirea defectarilor, sau corective atunci cand au ca scop depanarea sistemului, adica restabilirea starii de buna functionare dupa producerea unei defectiuni [5].

Scopul principal al activitatilor de mentenanta este asigurarea unei disponibilitati A(t) a sistemului cat mai ridicate. Pentru aceasta trebuie ca timpul T_m necesar pentru efectuarea unei activitati de mentenanta sa fie cat mai scurt. Timpul de mentenanta T_m este evident o variabila aleatoare ale carei valori depind de mentenabilitatea sistemului, de natura defectiunii sau cauzei care a impus efectuarea actiunii de mentenanta si de modul de organizare, pregatire si desfasurare a actiunilor de mentenanta.

Legea de repartitie a variabilei T_m, adica probabilitatea ca durata unei activitati de mentenanta sa nu depaseasca un anumit timp t dat, se numeste functie de mentenabilitate sau functie de mentenanta. Notand cu M(t) aceasta functie, rezulta:

M(t) = P .

Ea caracterizeaza atat mentenabilitatea sistemului cat si mentenanta sa (organizarea, pregatirea, desfasurarea si eficienta actiunilor de mentenanta).

Ca pentru orice variabila aleatoare, si pentru T_m se poate defini o densitate de repartitie , o intensitate a activitatilor de mentenanta:

Μ_m(t) =

si o durata medie a activitatilor de mentenanta:

M_m = = .

Daca se admite o repartitie exponentiala a duratelor de mentenanta rezulta:

M(t) = 1 - e , cu μ_m = constant si m_m = 1/ μ_m .

In multe cazuri, functia de mentenabilitate M(t) se refera doar la activitatile de mentenanta corective deoarece in general se admite ca activitatile preventive au o durata care nu este aleatoare, aceste activitati fiind planificate apriori.

Daca se presupune ca in urma activitatilor de mentenanta sistemul este redus la parametrii initiali devenind ca nou, atunci pentru studiul fiabilitatii (disponibilitatii) sistemului pot fi utilizate toate rezultatele din teoria restabilirii sau reinnoirii. In acest caz T_m = T_r , unde T_r este variabila aleatoare timp de restabilire si M(t) = G(t) , unde G(t) este legea de repartitie a lui T_r (vezi paragraful 11.2.1, relatiile (11.13) (11.14)).

Daca se considera ca in urma actiunilor de mentenanta sistemul nu devine ca nou, ci ramane vechi (sistem bun dar vechi) pastrandu-si uzura fizica si uzura fiabilistica (imediat dupa restabilirea sistemului, R(t) nu mai este 1) atunci pentru studiul disponibilitatii sistemului trebuie utilizate metode adecvate. Aceasta situatie apare insa rar in cazul sistemelor electronice datorita urmatoarelor motive: majoritatea componentelor electronice utilizate azi nu prezinta uzura fizica sau fiabilistica, lucru reflectat intr-o intensitate de defectare constanta in timp (repartitie exponentiala a timpului de buna functionare); in majoritatea cazurilor restabilirea sistemelor electronice se face prin inlocuirea componentelor necorespunzatoare cu componente noi.

In continuare se va face o analiza fizica a mentenabilitatii sistemelor electronice. Pentru inceput se vor considera numai activitatile de mentenanta corective si pentru comoditatea exprimarii, durata acestor activitati va fi denumita timp de restabilire (reinnoire) Tr. In mod evident, timpul de restabilire T_r depinde de natura defectiunii, de calificarea si de experienta depanatorilor si de solutiile constructive utilizate in realizarea sistemului. Natura defectiunii, ca si calificarea si experienta depanatorilor, determina timpul necesar pentru diagnosticarea si depistarea defectiunii, iar solutiile constructive determina in mod hotarator timpul de acces (de depistare fizica a defectiunii) , sau de interventie in sistem. Daca depanatorii sunt foarte buni, atunci timpii de restabilire sunt practic determinati de solutiile constructive utilizate in sistem. In cazul unor solutii constructive greoaie sau incomode, ca si in cazul unor depanatori cu experienta redusa, timpul de restabilire poate creste mult din cauza producerii in mod involuntar, in timpul interventiei in sistem, a unor defecte noi, suplimentare. Pentru sisteme electronice asemenea defecte se datoreaza in special solutiilor constructive insuficient studiate si pot fi de urmatorul gen:

contact imperfect in conectorul unui modul (placi, casete etc.) ca urmare a extragerii si introducerii modulului.

conductoare rupte in forma de cablu, ca urmare a tensionarii ei din diferite motive determinate de accesul in sistem; de regula, ruperile se produc in dreptul conexiunilor cu pinii conectoarelor, intrerupatoarelor, potentiometrelor etc.

scurtcircuit intre terminalele unor componente, ca urmare a modificarii involuntare a pozitiei unor piese componente sau ca urmare a caderii unor terminale metalice straine intre terminalele respective;

dereglari ale unor elemente de reglaj.

In aceste conditii este evident ca proiectantul unui sistem electronic trebuie sa adopte acele solutii constructive care sa asigure pe langa o fiabilitate cat mai mare si un timp de restabilire cat mai mic adica, o mentenabilitate cat mai mare. Fiabilitatea si mentenabilitatea apar astfel ca proprietati ale sistemului implementate de proiectant si constructor atat in fazele de conceptie, cat si in cele de realizare ale sistemului. Deoarece anumite restrictii de cost, greutate, gabarit, impiedica realizarea unei fiabilitati foarte mari, rezulta ca o atentie deosebita trebuie acordata mentenabilitatii. De aceea proiectantul unui sistem trebuie sa gaseasca solutii care sa ofere sistemului in primul rand o mentenabilitate ridicata si in al doilea rand o fiabilitate sporita, mai ales ca si cheltuielile pentru cresterea mentenabilitatii sunt in general mult mai mici decat cheltuielile pentru cresterea fiabilitatii.

Activitatile de mentenanta preventiva constau in inspectarea periodica, vizuala, a starii componentelor, conexiunilor si elementelor mecanice mobile, in corectarea celor care prezinta o stare necorespunzatoare si eventual in inlocuirea (reinnoirea) preventiva a unor componente sau a unor module.

Pentru un sistem dat, organizarea si planificarea judicioasa a activitatilor de mentenanta are un rol esential in obtinerea unei eficiente ridicate a sistemului.

Succesul in activitatile de mentenanta depinde de adoptarea unor strategii de reinnoire a elementelor defecte sau a celor care au functionat un timp determinat, precum si de adoptarea unor planuri de inspectie optime.

2. STRATEGII DE REINNOIRE

Se pot lua in consideratie urmatoarele strategii simple de reinnoire:

strategia A: o componenta se inlocuieste numai daca se defecteaza;

strategia B: o componenta se inlocuieste daca se defecteaza, sau daca indeplineste o anumita varsta v;

strategia C: o componenta se inlocuieste periodic la momente de timp planificate 0, d, 2d, 3d, ., sau de cate ori se defecteaza;

strategia D: o componenta se inlocuieste periodic, la momente de timp planificate 0, d, 2d, 3d, ., sau de cate ori se defecteaza, dar numai daca timpul ramas din momentul defectarii pana la cea mai apropiata inlocuire planificata depaseste o anumita valoare t_D prestabilita.

Strategia A este evident o strategie pur corectiva deoarece nu foloseste inlocuiri preventive, in timp ce celelalte strategii sunt atat corective, cat si preventive. In strategiile A si B toate momentele inlocuirilor corective sunt aleatoare, intrucat momentele inlocuirilor preventive sunt momente fixe, planificate apriori. Pentru a evidentia mai bine diferentele dintre aceste strategii, in figura 1 se prezinta pentru fiecare strategie in parte cate o diagrama posibila a evolutiei procesului de reinnoire in ipoteza ca timpul necesar pentru efectuarea unei reinnoiri este nul. Pe ordonata s-a prezentat timpul T_u de utilizare (functionare) al componentei, dupa ultima reinnoire.

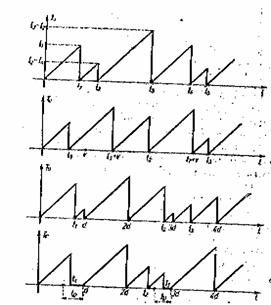
Fig. 1. Diagrame posibile pentru evolutia unui proces cu reinnoire instantanee considerand diverse strategii de reinnoire: a - strategie pur corectiva; b - strategie cu inlocuire dupa varsta; c - strategie rigida sau strategie

cu inlocuire in bloc; d - strategie rigida cu timp de asteptare.

Se observa ca in strategia B reinnoirile preventive se fac numai daca componenta a indeplinit varsta v, specificata, ceea ce permite o exploatare la maximum a componentelor dar nu permite o planificare exacta a momentelor de inlocuire preventiva. Spre deosebire de aceasta strategie, in strategiile C si D, momentele reinnoirilor preventive sunt strict planificate de la bun inceput, dar in schimb componentele nu mai sunt utilizate la maximum. Astfel, in strategia C o componenta reinnoita neplanificat (corectiv) la un moment anterior,dar apropiat de momentul unei reinnoiri preventive va fi din nou inlocuita cu ocazia reinnoirii preventive, desi a functionat foarte putin timp. Acest lucru constituie, din punct de vedere al costurilor, un dezavantaj important al strategie C in raport cu strategia B. Strategia C este totusi rationala daca reinnoirea preventiva are in vedere nu inlocuirea unei singure componente, ci inlocuirea intregului bloc din care face parte componenta, astfel incot, la "defectare" se inlocuieste doar componenta defecta, iar la momentul planificat se inlocuieste tot blocul, adica se reinnoiesc toate componentele sale. Pentru a reduce dezavantajul inlocuirii unor componente aproape noi, aceasta strategie se poate modifica introducand conditia ca la reinnoirile preventive, componentele bune care au functionat un timp scurt, inferior unei anumite durate, sa nu se mai inlocuiasca, sau introducand conditia ca reinnoirile corective (neplanificate) sa nu se mai faca. Daca timpul ramas pana la prima reinnoire planificata este inferior unei anumite valori t_D prestabilite.

Strategia a se foloseste de regula in cazul sistemelor formate din componente care au o intensitate de defectare z(t) ce nu depinde de timp, si implicit de varsta, deoarece in acest caz planificarea unor inlocuiri preventive nu este justificata, intrucat "pericolul de defectare" z(t) dt este acelasi tot timpul chiar daca se fac sau nu reinnoiri. Cu atat mai mult nu se justifica planificarea unor reinnoiri daca intensitatea defectiunilor este cazatoare in timp, deoarece imediat dupa reinnoire "pericolul de defectare" va fi mai mare decat inainte de reinnoire. Cum majoritatea componentelor electronice in conditii normale de utilizare au o intensitate a defectiunilor constanta in timp, rezulta ca strategia A este des aplicata in cazul sistemelor electronice, mai ales daca si functiile acestor sisteme nu sunt foarte importante.

Strategiile B, C, D se folosesc atunci cand aplicarea strategiei A conduce la costuri mari, sau atunci cand pretul componentelor este neinsemnat in raport cu pagubele pe care le-ar aduce defectarea lor, adica in cazul sistemelor de mare raspundere functionala. Aceste strategii sunt utile mai ales daca intensitatea defectiunilor este o functie care creste puternic in timp. In aceasta situatie se pot gasi si sistemele electronice deoarece in structura lor intra se regula si elemente mecanice sau electro-mecanice (comutatoare, relee, intrerupatoare, taste, conectori, potentiometre, motoare, micromotoare etc.) care au intotdeauna, datorita uzurii, o intensitate de defectare crescatoare in timp. In plus, daca sistemul electronic functioneaza in conditii climatice grele, puternic variabile si/sau in prezenta unor solicitari mecanice severe, ca de exemplu pe avioane sau vapoare, toate componentele electronice vor avea o intensitate de defectare crescatoare in timp.

In continuare se vor analiza si compara strategiile A, B, C, D din punct de vedere al costurilor, deoarece in majoritatea cazurilor acesta este criteriul pe baza caruia se alege o strategie sau alta Pentru aceasta se va considera ca reinnoirea se face instantaneu, intrucat timpul necesar pentru inlocuirea unei componente este de regula foarte mic in comparatie cu durata de buna functionare.

Se iau in considerare costurile:

c_n, costul unei inlocuiri (reinnoiri) corective sau neplanificate;

c_p, costul unei inlocuiri preventive sau planificate.

Este evident ca daca c_n < c_p, strategia A este net avantajoasa din punctul de vedere al costurilor fata de celelalte strategii. Daca c_n > c_p, pentru a putea compara strategiile intre ele trebuie determinate costurile medii pe unitatea de timp. Vom analiza aceste costuri pentru fiecare strategie in parte:

. In cazul strategiei A, costul mediu pe unitatea de timp este:

C_A = (1)

Deoarece in medie la fiecare interval de timp de durata m, egala cu media timpului de buna functionare, se produce o defectare si respectiv o reinnoire neplanificate.

. In cazul strategiei B, costul total pe un ciclu de reinnoire, adica intre doua reinnoiri succesive, va fi c_n daca apare o defectare inainte ca elementul sa indeplineasca varsta v, sau c_p daca elementul indeplineste varsta v. Probabilitatea ca elementul sa nu indeplineasca varsta v este F(v) = 1 - R(v), iar probabilitatea ca sa indeplineasca varsta v este R(v). Ca urmare, costul mediu total intr-un ciclu de reinnoire va fi:

c_n F(v) + c_p R(v) = c_n - ( c_n - c_p ) R(v)

Durata unui ciclu de reinnoire este v, cu probabilitatea R(v), sau x < v, cu probabilitatea f(x)dx. Cum x poate lua orice valoare in intervalul [0, v] rezulta ca durata medie a unui ciclu de reinnoire este :

V R(v) + = . (2)

unde integrala din membrul intai s-a efectuat prin parti.

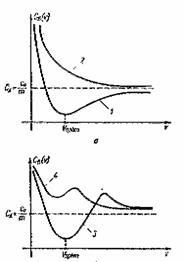
Fig. 2. Variatii posibile ale cheltuielilor medii in unitatea de timp in functie de varsta v, pentru strategia B.

Costul mediu pe unitatea de timp, in strategia B, va fi:

C_B = 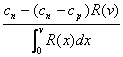    (3)

Se observa din relatia (3) ca daca v este mic ( R(v) 1 si v ) costul mediu pe unitatea de timp devine foarte mare si tinde la infinit cand v 0, ceea ce este intrutotul explicabil din punct de vedere fizic prin numarul foarte mare de reinnoiri preventive efectuate in unitatea de timp. Daca v este foarte mare si tinde la infinit ( R(v) 0 si m ) rezulta C_B ≈ C_A , ceea ce este iarasi explicabil deoarece pentru v strategia B se reduce la strategia A. pe baza acestor observatii se poate afirma ca graficul functiei C_B(v) poate avea sau forma 1 sau forma2 din figura 2, a. In principiu, graficul C_B(v) poate avea si forma 3 sau 4 din figura 2, b, sau alte forme, dar asa cum va rezulta din cele ce urmeaza formele cele mai probabile sunt 1 si 2.

In mod evident strategia B este sigur avantajoasa numai daca graficul C_B(v) are forma 1, adica daca pentru v foarte mare, C_B(v) este o functie crescatoare. Ca urmare, o conditie suficienta de eficienta a strategiei B va fi:

> 0 (4)

Din 3 rezulta:

= . (5)

Inlocuind f(v)=z(v)R(v) si deoarece R(v)>0, pentru orice v, rezulta conditia de eficienta:

> 0

sau :

(c_n - c_p) z()m - c_n > 0

adica:

m z() > . (6)

Conditia (6) este suficienta pentru ca strategia B sa fie superioara strategiei A. Ea va fi intotdeauna satisfacuta daca rata de defectare z(t) este o functie crescatoare nemarginita in timp. Acest lucru se intampla practic pentru marea majoritate a componentelor, mai ales, in perioada de batranete.

Daca acum se are in vedere graficul 3 din figura 2, b, rezulta ca in general conditia (6) este o conditie suficienta, dar nu absolut necesara pentru ca strategia B sa fie mai avantajoasa decat strategia A. In general deci pentru a aprecia eficienta strategiei B, va trebui studiat complet graficul lui C_B(v) sau va trebui rezolvata inegalitatea C_B(v) < C_A.

In cazul componentelor electronice aflate in perioada de viata normala se admite de obicei o repartitie exponentiala a duratei de functionare, cu z(t) = 1/m = constant. Ca urmare, conditia (6) nu poate fi satisfacuta deoarece intotdeauna > 1, ceea ce inseamna ca in cazul sistemelor electronice aflate in perioada de viata normala, utilizarea strategiei B nu are rost. Strategia B va fi insa utila daca exploatarea sistemelor electronice se va intinde ca durata si in perioada de "batranete".

Conform figurii 2 rezulta ca in general in strategia B exista o varsta optima v_optim , pentru care cheltuielile medii pe unitatea de timp sunt minime (mai ales daca este satisfacuta si conditia (6)). Notand v_optim = v* si anuland expresia (5), rezulta ca varsta optima la care trebuie facute inlocuirile preventive, satisface ecuatia:

z(v*)+ R(v*) = . (7)

care mai poate fi scrisa si astfel:

c_n - (c_n -c_p) R(v*) = (c_n - c_p)z(v*). (8)

Tinand cont de (3) si (8) rezulta ca in strategia B, daca exista v* , valoarea medie minima a costului pe unitatea de timp, este:

C_B*= C_B(v*) = (c_n - c_p)z(v*).   

unde v* se afla din ecuatia (7).

. In strategia C, cheltuielile medii totale pe un interval de durata d avand originea la momentele 0, d, 2d, 3d, . sunt c_n H(d) + c_p, unde H(d) reprezinta functia de reinnoire, adica numarul mediu de defectari, respectiv reinnoiri care au avut loc in intervalul de durata d. Ca urmare, costul mediu pe unitatea de timp va fi:

C_C = . (10)

Se observa usor ca daca d 0, C_C ∞ , iar daca d ∞ , conform proprietatii (11.30) rezulta ca

Cc C_A, rezultat firesc deoarece in acest caz strategia C se transforma in strategia A.

Judecand la fel ca in cazul strategiei B, o conditie suficienta de eficienta a strategiei C in raport cu strategia A, va fi:

_d > 0    (11)

ceea ce conduce, tinand cont de relatia (10) la:

> 0, (12)

unde h(d) reprezinta densitatea de reinnoire, adica numarul mediu de defectari, respectiv reinnoiri pe unitatea de timp.

Dar pentru d foarte mare, conform teoremelor asimptotice din teoria reinnoirii h(d) ≈ ≈,ceea ce implica :

[dh(d) - H(d)] = 0.

Ca urmare, conditiile (12), (11) nu vor fi satisfacute niciodata, ceea ce inseamna ca forma cea mai probabila pentru graficul C_C(d) este forma 3 din figura 2, b unde in locul lui v trebuie considerat d.

Notand cu d* valoarea optima a lui d (perioada optima a inlocuirilor preventive), care asigura cheltuieli minime, si anuland derivata functiei C_C(D) rezulta ca d* (ca si orice punct de extrem al functiei) satisface ecuatia:

d* h(d*) -H(d*) = . (13)

O conditie suficienta de existenta a perioadei optime d este ca densitatea de reinnoire h(t) sa fie o functie crescatoare. Valoarea medie minima a costului pe unitatea de timp in strategia C, se obtine din relatia (10), tinand cont de relatia (13). Rezulta:

C = C_C(d*) = c_nh(d*), (14)

unde d este acea solutie a ecuatiei (13), pentru care derivata lui Cc(d) trece de la valori negative la valori pozitive.

Deoarece conditia (11) nu permite, la fel ca in cazul strategiei B, strategia unui criteriu de eficienta al strategiei C in raport cu strategia A, pentru a stabili un asemenea criteriu trebuie rezolvata inegalitatea C_C(d) < C_A. In acest scop, pentru functia de reinnoire H(t) se poate utiliza urmatoarea estimatie, valabila pentru timpi mari [4, pag. 148]

H(t) ≈ + ,

unde m si reprezinta media si respectiv dispersia variabilei aleatoare care genereaza procesul de reinnoire; in cazul nostru, variabila generatoare este timpul T de buna functionare a elementului analizat.

Folosind pentru aceasta estimatie impreuna cu relatia (10) ci conditia C_C <C_A = , rezulta ca strategia C este preferabila strategiei A, daca:

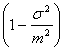> . (15)

Daca aceasta conditie este indeplinita, atunci se poate trece la rezolvarea ecuatiei (13) di aflarea lui d*. rezolvarea ecuatiei (13) este in principiu simpla deoarece se cunoaste modul de calcul al functiilor h(t) si H(t) pornind de la f(t) si F(t) (v. relatiile (11.27) (11.28)). In cazul distributiei Weibull insa calculul lui h(t) si H(t) fiind dificil, se va indica in continuare o metoda aproximativa de determinare a perioadei optime d*. In cazul unei rate de defectare crescatoare sunt valabile inegalitatile:

C_C0(d) ≤ C_C(d) ≤ C_C2(d)

unde:

C_C0(d)=

reprezinta costul mediu pe unitatea de timp intr-o strategie de perioada d, in care se face o singura reinnoire corectiva intre doua reinnoiri preventive

CC2(d)= 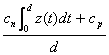reprezinta costul mediu pe unitatea de timp intr-o strategie de perioada d, in care repararile (repunerile in stare de functie) efectuate intre doua reinnoiri preventive nu schimba uzura fiabilistica a sistemului (sistemul reparat este bun dar vechi; acest caz difera de cazul general al reinnoirilor cand sistemul devine bun si nou).

Minimizand pe C_C0(d), rezulta valoarea optima d din relatia:

df(d) - F(d) = .

Minimizand C_C2(d) , rezulta valoarea optima d din relatia:

dz(d) - =.

Valorile d si d se pot calcula cu usurinta, iar valoarea optima d* se alege prin doua-trei incercari intre aceste valori.

. In cazul strategiei D, pentru determinarea costurilor totale pe un interval de durata d dintre doua reinnoiri preventive, trebuie sa tinem cont si de pierderile (costurile) provocate de nefunctionarea elementului in intervalul de asteptare.

Deoarece in medie evenimentele care au loc pe intervalul de durata d dintre doua reinnoiri preventive sunt aceleasi, indiferent de pozitia intervalului pe axa timpului, in continuare se va considera procesul de reinnoire in intervalul [0, d] - figura 3.

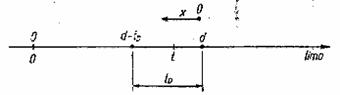
Fig. 3. Schita ajutatoare pentru studiul strategiei D.

Conform strategiei D, pe acest interval vor avea loc reinnoiri corective neplanificate numai pana la momentul (d - t_D), unde t_D reprezinta durata maxima admisa a intervalului de asteptare. Numarul acestor reinnoiri va fi in medie H(d - t_D), iar cheltuielile asociate lor vor fi c_nH(d - t_D). Dupa momentul (d - t_D) reinnoirile corective se sisteaza (se stopeaza) astfel ca elementul care se defecteaza este lasat sa astepte momentul reinnoirii preventive. Daca notam cu t momentul defectarii elementului, durata intervalului de asteptare va fi:

x =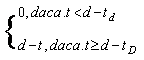

Intr-un proces continuu de reinnoire, probabilitatea ca la un moment t sa apara o defectare si respectiv o reinnoire este h(t)dt. In cazul analizat de noi procesul de reinnoire nu mai este un proces continuu, ci un proces stopat [4], deoarece dupa momentul (d - t_D) reinnoirile inceteaza. Ca urmare, probabilitatea ca la momentul t sa apara o defectare va fi h(t)dt daca t < d - t_D, si respectiv h(t)R(d - t)dt, [3], daca t > d - t_D.

Valoarea medie a intervalului de asteptare va fi:

_{= .}

Cu schimbarea de variabila d - t = x, rezulta:

_.

Notand cu c_i cheltuielile sau pierderile pe unitatea de timp determinate de nefunctionarea elementului, costul mediu corespunzator unei perioade de asteptare va fi c_i iar costul mediu total pe unitatea de timp in strategia D, va fi:

C_D = . (16)

Un caz mai general, in cadrul strategiei D, apare atunci cand costul corespunzator inactivitatii pe un interval de durata x este de forma c_i0 + c_ix. In acest caz, rezulta:

C_D = . (17)

Se poate ca in acest caz strategia D este preferabila strategiei C numai daca c_i0 < c_n deoarece in acest caz contrar utilizarea unui interval de inactivitate costa mai mult decat o reinnoire neplanificata. Intr-adevar, deoarece C_D(t_D=0)=C_C rezulta ca pentru ca strategia D sa fie preferabila strategiei C trebuie ca C_D(t_D) sa fie o functie scazatoare, adica trebuie ca <0, ceea ce conduce la c_i0 < c_n.

Daca c_i0= 0, atunci intotdeauna este profitabila alocarea unui timp de asteptare.

Deoarece din motive economice si functionale, durata maxima a intervalului de asteptare (x_max=t_D) nu poate fi prea mare, rezulta ca intotdeauna x este suficient de mic, astfel ca in expresiile anterioare se poate considera R(x) 1. Din punct de vedere fizic, acest lucru este justificat deoarece daca un proces continuu de restabilire este stopat pe un interval mic de timp, probabilitatea de defectare in intervalul de stopare va fi practic aceeasi cu cea din cazul procesului continuu (h(t)dt) deoarece in acel mic interval de timp in procesul continuu de reinnoire nu pot avea loc atat de multe reinnoiri incot probabilitatea de defectare ulterioara sa se schimbe considerabil fata de cazul procesului stopat.

Valoarea optima t a lui t_D care asigura minimum de cheltuieli rezulta din ecuatia:

= (18)

unde se poate considera R(t) Ca urmare, se obtine:

t = . (19)

Daca t_D este suficient de mic, se poate considera ca h(t) variaza putin pe intervalul t_D si functia h(d - x) din relatia (17) poate fi tratata ca o constanta h(d). De asemenea, daca t_D este mic, H(d - t_D) poate fi aproximat, trecand de la diferentiala la diferente finite:

H(d - t_D) ≈ H(d) - t_Dh(d).

Ca urmare, expresia (17) devine:

CD(d, t) ≈ Cc(d) -

Unde C_C(d) reprezinta costul mediu pe unitatea de timp in strategia C (10).

Pentru t_D = t rezulta:

C_D(d,- (21)

Daca d nu este prea mic, se poate inlocui h(d) cu valoarea limita 1/m.

Considerand pentru d valoarea d* corespunzatoare optimului in strategia C, din (12), (14) si (19) se obtine:

C_D(d*,)≈ .

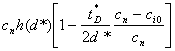Toate relatiile anterioare capata o forma mai simpla daca c_i0 = 0, sau daca c_i0 << c_n. In acest caz:

si

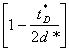C_D(d*,) C_C(d*) (23)

Pentru a lua o decizie privind adoptarea uneia din strategiile A, B, C sau D, trebuie sa se compare costurile medii in variantele lor optime (minime). Deoarece strategia D este practic o varianta a strategiei C, mai eficienta decat aceasta daca este indeplinita conditia c_n > c_i0, in continuare este suficient sa se compare doar strategiile A, B, C. In acest scop, trebuie sa se tina cont de faptul ca i n general costul unei reinnoiri planificate c_p nu este acelasi in strategiile B si C. Ca urmare se va nota cu c_pB si respectiv c_pC costul mediu al unei reinnoiri planificate in strategia B respectiv C; in general c_pB > c_pC. Folosind relatiile (1), (9), (14) se pot scrie costurile minime normate la costul mediu al unei reinnoiri corective, pentru cele trei strategii.

Rezulta:

(24 a)

(24 b)

(24 c)

unde:

a=

Duratele optime v*, d* se obtin rezolvand ecuatiile (7), (13), care mai pot fi scrise astfel:

(26 a)

(26 b)

unde:

(27)

Costurile minime k_B si k_C sunt functii numai de a, respectiv b. Deoarece intotdeauna costurile vor creste daca costul unei reinnoiri planificate (cp) creste, rezulta ca functiile k_B(a) si k_C(b) sunt functii monoton crescatoare. Ca urmare, din ecuatiile:

; (28)

se pot afla valorile limita a₀, respectiv b₀ deasupra carora strategiile B respectiv C devin nerentabile in raport cu strategia A.

Pentru un element dat cu parametrii de fiabilitate cunoscuti, valorile a₀ si b₀ sunt constante caracteristice ale elementului respectiv si care nu au nici o legatura cu costul reinnoirilor sau cu strategia adoptata.

Asadar, pentru un element dat se pot calcula valorile caracteristice a₀ si b₀ , rezolvand ecuatiile (28), iar pentru oricare din strategiile A, B, C se poate calcula parametrii a si b conform relatiilor (25), (27). In functie de ordonarea a, a₀ si b, b₀ se poate lua decizia pentru alegarea strategiei optime care determina cele mai mici cheltuieli. Astfel:

daca a > a₀ si b > b₀ , strategia optima este strategia A;

daca a < a₀ si b > b₀ , strategia optima este strategia B;

daca a > a₀ si b < b₀ , strategia optima este strategia C;

daca a < a₀ si b < b₀ , atat strategia B cat si strategia C sunt mai rentabile decat strategia A.

Pentru aflarea celei mai rentabile strategii se pot calcula si compara direct costurile normate k_B, k_C sau se poate utiliza urmatorul procedeu general:

din egalitatea k_B(a) = k_C(b) se determina dependenta b* = b*(a) care reprezinta relatia de legatura necesara intre b si a pentru a avea cheltuieli egale in cele doua strategii. Trebuie observat ca b*(a₀)=b₀ deoarece si daca b(0) = 0, ceea ce inseamna ca graficul functiei b*(a) trece prin origine si prin punctul de coordonate (a₀, b₀) - figura 4.La fel ca si valorile a0, b0 curba cu functia b* = b*(a) este, pentru un element dat, o marime caracteristica proprie , dependenta doar de fiabilitatea acestuia. Pentru o strategie B data valoarea a se cunoaste si deci se poate determina valoarea corespunzatoare b*(a) . Pentru o strategie C data, valoarea b este de asemenea cunoscuta. Daca b > b*(a), adica daca in figura 4 punctul de coordonate (a, b) cade deasupra curbei b*(a) strategia optima este strategia B. Daca b<b*(a), adica daca punctul de coordonate (a, b) cade sub curba b*(a), strategia optima este strategia C. Daca b=b*(a), ambele strategii sunt la fel de eficiente.

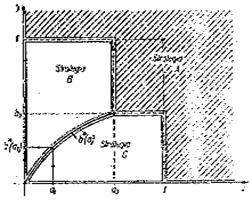
Fig. 4. Alegerea strategiei optime de reinnoire pe baza costurilor minime:

Strategia A - strategie pur corectiva;

Strategia B - strategie cu inlocuire dupa varsta;

Strategia C - strategie cu inlocuire in bloc.

In figura 4 pentru strategiile de reinnoire A, B, C se reprezinta sugestiv toate situatiile legate de alegerea strategiei optime. Pe baza acestora, cat si pentru a evita determinarea analitica a functiei b*(a) , se poate construi urmatorul algoritm de alegere a strategiei optime:

Pentru elementul supus procesului de reinnoire se determina valorile a₀, b₀ si eventual functia b*(a).

Pentru strategiile A, B, C date se determina valorile a, b corespunzatoare.

Daca a > a₀ si b > b₀ strategia optima este A; STOP.

Daca a < a₀ si b > b₀ strategia optima este B; STOP.

Daca a > a₀ si b < b₀ strategia optima este C; STOP.

Daca a < a₀ si b < b₀ se urmeaza pasii 4 . 7.

Din relatia (6 a) se calculeaza varsta optima v*, iar din relatia (6 b) se determina costurile k_B(v*) corespunzatoare varstei v*.

Utilizand relatia (26 c) si punand conditia k_B(v*) = k_C(d*) se calculeaza valoarea d* care determina costurile egale in strategiile B si C.

Introducand valoarea d* calculata la pct. (5) in expresia (26 d) rezulta criteriul de decizie b*.

Daca b > b*, strategia optima este B; STOP.

Daca b < b*, strategia optima este C; STOP.

Variante ale strategiilor de reinnoire prezentate se pot construi modificand criteriul de alegere al momentelor de reinnoire sistematica. Pana aici criteriul de alegere pentru aceste momente a fost minimizarea costurilor. Se pot utiliza insa drept criteriu, asigurarea unei anumite fiabilitatea sau disponibilitatea pe intervalul dintre doua reinnoiri, sau mai general conditia de extrem pentru o marime dependenta de v, respectiv d.

Ca exemplu, se va prezenta cazul strategiei B atunci cand se doreste maximizarea disponibilitatii in raport cu strategia A.

Pentru precizarea disponibilitatii este necesar sa se cunoasca durata reinnoirilor. Fie m_n durata medie a unei reinnoiri neplanificate (corective) si fie m_p durata medie a unei reinnoiri preventive.

In cazul strategiei A, coeficientul de disponibilitate este:

A_A =

unde m este durata medie de buna functionare a elementului considerat.

In cazul strategiei B, coeficientul de disponibilitate pe intervalul dintre doua reinnoiri va fi:

A_B = . (29)

Punand conditia se poate gasi valoarea optima a lui v, daca bineinteles aceasta exista.

Pentru ca strategia B sa fie superioara strategiei A, este necesar ca A_B > A_A, ceea ce conduce la:

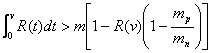. (30)

Deoarece m = , rezulta ca o conditie absolut necesara (dar nu si suficienta) pentru a satisface inegalitatea (30) este ca paranteza mare din aceasta inegalitate sa fie subunitara ceea ce implica m_p <m_n. Din punct de vedere fizic, aceasta conditie este evidenta deoarece in caz contrar reinnoirile preventive nu mai au rost.

Pentru v → ∞ , strategia B tinde spre strategia A si deci A_B → A_A. Pentru v → 0 din relatia (29) rezulta ca A_B → 0. Ca urmare, graficul functiei A_B(v) poate avea una din formele prezentate in figura 5. Considerand forma 1, rezulta ca o conditie suficienta ca strategia B sa fie superioara strategiei A este:

ceea ce conduce, dupa efectuarea calculelor, la:

. (31)

Aceasta conditie va fi satisfacuta intotdeauna daca rata defectiunilor z(t) este nemarginit crescatoare si daca m_n > m_p.

Considerand curba 3 si inegalitatea (30) se poate arata ca strategia B va fi superioara strategiei A, daca rata de defectare este o functie crescatoare cu limita finita l care satisface conditia:

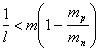. (32)