Stabilitatea echilibrului elastic - Formula lui Euler

Stabilitatea echilibrului elastic

Cuprins:

Generalitati

Calculul sarcinii critice de flambaj pentru bara comprimata, dublu articulata.

Formula lui Euler

Limitele de aplicare ale formulei lui Euler. Flambajul in domeniul plastic

Calculul la flambaj folosind coeficientul de zveltete, l

Calculul la flambaj folosind metoda coeficientului de flambaj, j

1. Generalitati

In cadrul solicitarii de intindere-compresiune centrica nu s-a analizat comportarea la compresiune a barelor zvelte (bare cu lungime mare in comparatie cu dimensiunile sectiunii transversale). Aceste bare prezinta particularitatea ca, pentru anumite valori ale fortei de compresiune, fara a se depasi rezistenta admisibila la compresiune, isi pot pierde forma initiala de echilibru. Deci forma initiala de echilibru poate fi stabila sau instabila.

Pozitia de echilibru este stabila daca prin modificarea acesteia, cu valori mici, sistemul revine la pozitia de echilibru (sau oscileaza in jurul acesteia).

Daca sistemul nu are aceasta proprietate, prin scoaterea din pozitia de echilibru, cu valori mici ale deplasarilor, el nu mai revine in acea pozitie, putand suferi deformatii mari care sa duca la distrugerea sa.

Pierderea stabilitatii sistemelor deformate (bare, sisteme de bare, placi) sub actiunea fortelor se numeste flambaj.

Un caz des intalnit in practica este acela al flambajului barelor drepte, solicitate la compresiune.

Pentru bara dreapta zvelta din fig. 1, sub actiunea fortei de compresiune, se dezvolta tensiunea s < 0. Daca forta atinge o anumita valoare, , numita forta critica de flambaj , bara isi pierde forma dreapta de echilibru si, deci, flambeaza.

Figura 1

Fortei critice ii corespunde o tensiune normala critica de flambaj, , ce se calculeaza cu expresia:

(1)

unde A este aria sectiunii transversale, considerata constanta, a barei.

Bara nu va flamba daca este comprimata cu o forta, P, mai mica decat cea critica:

(2)

unde este un coeficient de siguranta la flambaj.

Pericolul deosebit al flambajului consta in faptul ca el se produce in mod brusc si nu mai permite executarea unor lucrari de consolidare.

S-au elaborat diferite teorii de calcul la flambaj, dintre care unele conduc la ecuatii diferentiale neliniare complicate.

2. Calculul sarcinii critice de flambaj pentru bara comprimata, dublu articulata. Formula lui Euler

Exista mai multe metode de calcul a fortei critice de flambaj, cum ar fi metoda statica, metoda energetica, metoda aproximatiilor succesive, metoda dinamica, s.a. Pentru prima data aceasta forta s-a calculat de catre L. Euler (anul 1744).

In continuare se va determina forta critica de flambaj folosind metoda statica. Fie cazul unei bare zvelte dublu articulata la capete, de rigiditate constanta, EI, in fiecare sectiune transversala. Ea se comprima centric cu forta critica de flambaj, . Ca urmare bara capata forma deformata, adica flambeaza, ca in fig. 2.

In sectiunea transversala, situata la distanta x de articulatia A, se dezvolta momentul incovoietor:

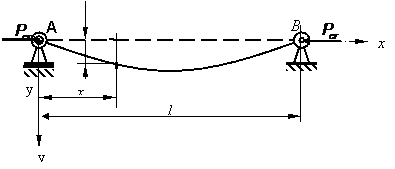
Figura 2

Ecuatia diferentiala a fibrei medii deformate devine:

Se noteaza , iar ecuatia devine:

(3)

Aceasta ecuatie diferentiala omogena, de ordinul doi, are solutia:

Cu conditiile de legatura: v (0) = v (l) = 0, rezulta:

Cum trebuie sa fie diferita de zero (pentru a se realiza pozitia deformata a barei), trebuie indeplinita conditia:

sin kl = 0 sau kl = np , n = 1,2, 3, . . .

Deci forta critica de flambaj este:

(4)

Pentru n = 1 se realizeaza starea de flambaj din figura 2. Celelalte solutii, (n= 2,3, . .), conduc la valori mai mari ale fortei critice, care nu se mai ating, deoarece flambajul s-a atins pentru forta cea mai mica.

In relatia (5) momentul de inertie I al sectiunii transversale corespunde directiei fata de care flambeaza bara. Daca bara poate flamba pe orice directie, atunci se ia in calcul , deoarece flambajul se produce in jurul acelei axe pentru care rigiditatea este minima.

Cu toate aceste observatii, formula lui Euler, pentru calculul fortei critice de flambaj, in cazul fundamental este:

(5)

In acest caz starea deformata are forma unei semiunde, de lungime egala cu lungimea barei. Aceasta lungime se numeste lungime de flambaj,

Formula pentru calculul fortei critice de flambaj, pentru bara dublu articulata, devine:

(6)

Daca bara are o articulatie la mijloc, se vor forma doua semiunde, deci , iar formula pentru calculul fortei critice de flambaj devine:

(7)

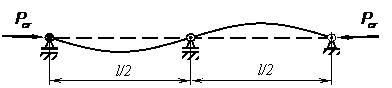
Cazul acesta este ilustrat in fig. 3.

Figura 3

Se obtin relatii asemanatoare pentru cazul cand bara prezinta doua, trei,sau mai multe articulatii.

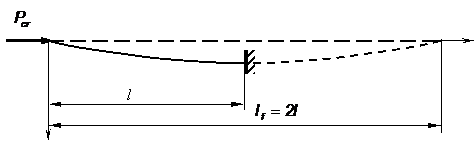
Se va considera in continuare cazul barei incastrate la un capat si libera la celalalt, solicitata la compresiune (fig. 4).

Figura 4

Se constata ca se poate obtine cazul fundamental, al barei dublu articulate, daca bara ar avea lungimea dubla; deci, in acest caz, lungimea de flambaj este

Formula pentru calculul fortei critice, pentru acest caz, va fi:

(8)

Se demonstreaza ca in cazul barei dublu incastrate (fig.5), lungimea de flambaj este .

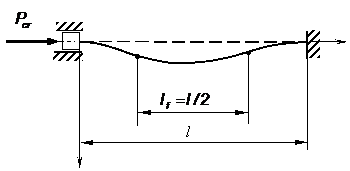
Figura 5

Deci :

(9)

Pentru cazul barei incastrata la un capat si articulata la celalalt (fig. 6), lungimea de flambaj este

Ca urmare, pentru bara comprimata, cu astfel de legaturi:

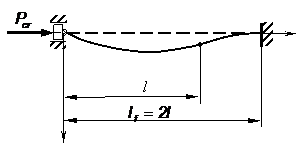
(10)

Figura 6

In rezumat, forta critica de flambaj se calculeaza cu expresia lui Euler:

(11)

in care este lungimea de flambaj, care depinde de modul de rezemare la capete a barei; acesta lungime este:

pentru bara incastrata la un capat si libera la celalalt;

pentru bara dublu articulata;

pentru bara incastrata la un capat, articulata la celalalt;

pentru bara dublu incastrata.

In aceste relatii l este lungimea barei, iar I este momentul de inertie al sectiunii transversale in raport cu axa in jurul careia se produce flambajul. Daca flambajul este posibil pe orice directie, se ia in calcul , deoarece flambajul se va produce dupa o directie pe care rigiditatea la incovoiere este minima (corespunzator unei forte minime de compresiune).

Problema nr.50

Pentru stalpul incastrat din figura se cere forta critica de flambaj. Stalpul este confectionat din profil I 20 (fig. 7) , cu si .

Rezolvare

Din tabelele de profile laminate, pentru I 20 se gasesc urmatoarele caracteristici geometrice:

A = 33,5 cm; Iz = 2140 cm ; Iy = 117 cm;

Se foloseste formula lui Euler :

, in care:

; ;

Figura 7

Se produc eforturi unitare normale de compresiune :

3. Limitele de aplicare ale formulei lui Euler.

Flambajul in domeniul plastic

Pentru bare drepte comprimate, legaturile permitand flambajul pe orice directie, s-a dedus formula lui Euler pentru calculul fortei critice de flambaj:

(12)

Acestei forte ii corespunde o tensiune normala de compresiune:

(13)

S-a definit raza de inertie a sectiunii transversale a barei ca fiind:

i = ,

deci se poate deduce raza de inertie minima:

(14)

Ca urmare, tensiunea de compresiune, pentru forta critica de flambaj devine:

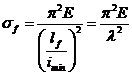(15)

unde s-a notat:

l (16)

Coeficientul l definit prin relatia (16) se numeste coeficient de subtirime sau coeficient de zveltete.

Relatia (15) arata dependenta dintre tensiunea normala la flambaj si coeficientul de zveltete, care este hiperbolica. Pe aceasta curba, numita hiperbola lui Euler, se disting doua zone:

- zona AB, pe care si corespunde flambajului in domeniul elastic, pentru care este valabila legea lui Hooke. Punctului B ii corespunde un coeficient

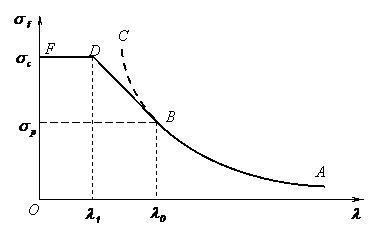
- zona BC, pe care si corespunde flambajului in domeniul plastic. Pe aceasta zona (fig. 8).

Figura 8

Formula lui Euler este valabila pe zona flambajului elastic, deci pentru

Pentru aflarea valorii coeficientului , in cazul barelor confectionate din , considerand , se obtine:

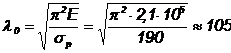
Pentru valori , tensiunea critica, , nu mai corespunde hiperbolei lui Euler. Aceasta tensiune se determina cu formule empirice care stabilesc o relatie intre si l, in zona flambajului plastic.

Unele din cele mai cunoscute sunt formulele Tetmajer - Iasinski, care stabilesc o relatie liniara de forma:

(17)

corespunzatoare dreptei BD. Punctul D corespunde valorii , respectiv unui coeficient de zveltete

Pentru se considera ca bara nu mai flambeaza, calculul facandu-se la compresiune simpla.

Coeficientii a si b variaza de la un material la altul. In tabelul urmator se dau coeficientii a, b, si pentru cateva materiale:

Pentru fonta se foloseste relatia:

, cu limitele si (18)

4. Calculul la flambaj folosind coeficientul de zveltete, l

Calculul la flambaj consta fie in a dimensiona o bara, daca se da coeficientul de siguranta la flambaj, , fie in a verifica valoarea coeficientului , daca celelalte elemente sunt cunoscute. Valorile coeficientului sunt foarte variate si nu exista prescriptii standardizate pentru ele. Ele pot fi intre 4 si 28, functie de importanta si pozitia piesei comprimate.

Astfel, pentru biela motoarelor de automobil = 4 ~ 5,5, iar pentru biela motoarelor termice mari

Calculul de verificare se incepe cu determinarea coeficientului de zveltete, l Functie de valoarea acestuia exista trei situatii:

- daca , atunci calculul continua folosind formula lui Euler, , iar echilibrul este stabil daca , unde este coeficientul de siguranta admis;

- daca , se utilizeaza relatii de calcul in domeniul plastic:

, apoi , respectiv

- daca , atunci bara nu flambeaza, iar calculul se face numai la compresiune.

In mod asemanator se determina forta capabila a barei (), sau lungimea admisa a barei.

Calculul de dimensionare la flambaj este mai dificil, deoarece nu se poate aprecia de la inceput in ce domeniu de flambaj se va situa bara, dupa efectuarea dimensionarii. De aceea se dimensioneaza bara cu formula de calcul a unui domeniu, de obicei cu formula lui Euler:

(19)

Dupa alegerea dimensiunii sectiunii transversale, trebuie efectuat un calcul de verificare, determinandu-se in primul rand coeficientul de zveltete, l

Daca , atunci formula lui Euler a fost bine aplicata, iar calculul a fost efectuat corect.

Daca , se va verifica sectiunea barei cu ajutorul relatiilor de calcul in domeniul flambajului plastic. In cazul in care se obtine se maresc dimensiunile sectiunii transversale si se reface calculul de verificare pana cand se obtine coeficientul de siguranta la flambaj admis.

Daca , flambajul nu se poate produce, iar calculul se face la compresiune.

Problema nr.51

Sa se dimensioneze o bara de otel de sectiune circulara, din OL 37, comprimata cu o forta P = 135 000 N, daca se impune un coeficient de siguranta la flambaj . Bara este articulata la capete si are lungimea: a) l = 1,8 m ; b) l = 0,8 m;

In domeniul flambajului plastic () se va utiliza formula: (

Rezolvare:

a)

Rezulta :

Pentru verificare, se calculeaza:

Prin urmare diametrul d = 60 mm poate fi acceptat, relatia lui Euler fiind corect utilizata.

b)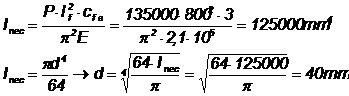

Pentru verificare:

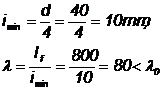
Asadar formula lui Euler nu este aplicabila. Se va face calculul cu formule pentru flambajul in domeniul plastic:

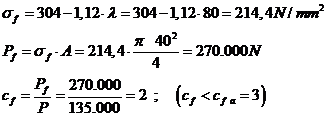
Rezulta ca diametrul trebuie marit. Se alege,de exemplu, d=48 mm .

Se reface calculul:

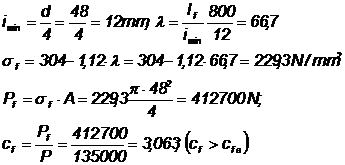
Rezulta ca diametrul de 48 mm poate fi acceptat.

5 Calculul la flambaj folosind metoda coeficientului de flambaj,

Metoda lui Euler de calcul la flambaj al barelor drepte comprimate are dezavantajul ca utilizeaza relatii de calcul diferite, dependente de coeficientul de zveltete, l. Acest inconvenient se poate elimina utilizand in calcule o rezistenta admisibila la flambaj, , care tine seama de pericolul pierderii stabilitatii, calculul reducandu-se la cel al compresiunii simple .

Pe baza acestei metode, conditia de stabilitate a barei comprimate se exprima prin relatia:

unde P este forta de compresiune, iar A este aria sectiunii transversale a barei.

Rezistenta admisibila la flambaj, , se calculeaza in functie de rezistenta la compresiune simpla, , si de un coeficient, j numit coeficient de flambaj, subunitar, cu atat mai mic cu cat pericolul de flambaj este mai mare:

(21)

Valoarea coeficientului j depinde de coeficientul de zveltete, l. In fig. 9 se arata grafic aceasta dependenta.

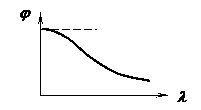
Figura 9

In normative se dau valorile coeficientului j pentru diferite materiale (STAS 763 /1-71) .

Cu expresia (21), conditia de stabilitate devine:

(22)

Relatia (22) se utilizeaza in special pentru calcule de verificare sau de determinare a fortei capabile.

La dimensionare, relatia are doua necunoscute, A si j, dependente una fata de alta. Calculul se face prin incercari.

Problema nr. 52

Se cere valoarea fortei de compresiune P, care se poate aplica unui stalp de fonta de inaltime l = 2 m, incastrat, de sectiune circulara, cu diametul d = 200 mm. Se cunoaste rezistenta admisibila la compresiune

Rezolvare

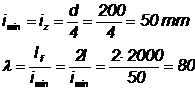
Din standarde se gaseste, pentru , valoarea coeficientului de flambaj, j

Forta capabila a stalpului este:

P = 3.330.000 N

Problema nr. 53

Sa se determine sarcina critica de flambaj pentru o bara de lemn de sectiune dreptunghiulara 8 cm x12 cm si lungime l=2 m, stiind ca este articulata la un capat si incastrata la celalalt.

Rezolvare:

Pentru cazul de rezemare din problema, rezulta ca lungimea de flambaj este:

;

; ;

;

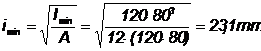Se aplica formula Tetmajer-Iasinski (anexa ):

163872 N

Rezulta:

68160 N