Cunoasterea caracteristicilorinstrumentelor/aparatelor

de masurare este esentiala pentru utilizarea optima a acestora.

CARACTERISTICI STATICE sI DINAMICE aparatelor de masurare

Elementele componente ale unui sistem de masurare, ca si sistemele de masurare in ansamblu, se caracterizeaza printr-un comportament specific in regim stationar si prin alt comportament specific in regim tranzitoriu. Comportarea in regim stationar se pune in evidenta prin ceea ce se numesc caracteristici statice.

Caracteristicile statice includ date privind marimile de intrare, date privind marimile de iesire, precum si relatii intre marimile de intrare si marimile de iesire ale elementelor sau sistemelor la care se refera. Relatiile dintre intrari si iesiri sunt de obicei functii algebrice continui sau discontinui si se folosesc mai ales sub forma grafica. Ele descriu dependenta iesirilor de intrari, facand abstractie de timp, deoarece pentru masurari statice se presupune ca pe timpul masurarii marimea masurata ramane constanta.

Prin caracteristici statice poate fi analizata si comportarea in regim periodic constant, cand marimile periodice au forma, amplitudinea, frecventa si faza constante. Prin urmare, ceea ce este definitoriu pentru regimul stationar este stationaritatea marimilor caracteristice in timp.

Comportarea elementelor si sistemelor in regim dinamic (tranzitoriu) se caracterizeaza prin modificarea marimilor in timp, mai precis, prin modificarea marimilor pe durata tranzitiei de la un regim stationar la altul. Un astfel de comportament se descrie prin ceea ce se numesc caracteristici dinamice.

Caracteristicile dinamice cuprind date privind marimile de intrare, date privind marimile de iesire, precum si relatii privind dependenta dintre marimile de intrare si cele de iesire pe timpul regimului tranzitoriu. Datorita variabilitatii marimilor de intrare si de iesire in timp, relatiile dintre aceste marimi in regim dinamic sunt descrise de ecuatii diferentiale. Astfel de relatii pot fi descrise si cu ajutorul unor functii de transfer dinamic care sunt functii de variabila complexa deduse din ecuatii diferentiale prin transformare Laplace sau alta transformare operationala.

1. CARACTERISTICI STATICE

Cele mai importante caracteristici statice sunt:

caracteristicile de transfer;

caracteristicile de intrare;

caracteristicile de iesire;

caracteristici de constructie si de exploatare.

1.1. Caracteristici de transfer

Sub aspect functional, un aparat de masurare (AM) sau o instalatie de masurare (IM) poate fi simbolizata, ca in figura 1. Aici x este marimea de masurat (intrare), y este marimea masurata (rezultatul masurarii), p₁, p₂ ,, p_n sunt factori perturbatori externi (temperatura, presiunea, umiditatea, campurile electrice si magnetice parazite) iar i₁, i₂ ,, i_m sunt factori perturbatori interni (frecarile, jocurile in lagare, modificarea proprietatilor materialelor si ale componentelor prin imbatranire), iar c₁, c₂ ,, c_p sunt comenzi pregatitoare pentru o masurare corecta.

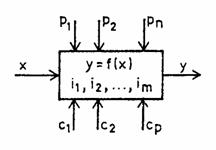
Fig.1. Marimi caracteristice ale unui AM.

Caracteristica de transfer ideala. In mod ideal, in regim stationar cand in timpul masurarii atat marimea x cat si marimea y raman neschimbate, dependenta dintre aceste marimi poate fi exprimata printr-un model matematic de forma:

(1)

Aceasta dependenta reprezinta ceea ce se numeste caracteristica de transfer ideala. Ea se stabileste teoretic pe baza legilor fizice care stau la baza functionarii aparatului sau instalatiei de masurare ori se stabileste experimental in conditii ideale de masurare, cand influenta factorilor perturbatori este complet anihilata.

Caracteristica de transfer reala. Marimea y depinde nu numai de marimea x ci si de alti factori perturbatori: p₁, p₂ ,, p_n si i₁, i₂ ,, i_m. Toti acesti factori perturbatori externi si interni constituie surse de erori de masurare, care produc erori de influenta si fac astfel ca marimea obtinuta in urma masurarii sa depinda de ei:

. (2)

Aceasta relatie exprima deci caracteristica statica de transfer reala a aparatului sau instalatiei de masurare.

Forma cea mai convenabila a caracteristicii de transfer ideale este cea liniara:

(3)

sau

. (4)

Exista insa si aparate cu caracteristica de transfer neliniara, ca de exemplu ampermetrele feromagnetice, la care iesirea a este proportionala cu patratul curentului i, adica

(5)

In tabela 1 sunt prezentate cinci dintre caracteristicile de transfer reprezentative pentru aparatele de masurare analogice.

Unele aparate de masurare ofera posibilitatea efectuarii unor operatii sau comenzi menite sa le pregateasca in vederea efectuarii unor masurari corecte. In figura 1 aceste comenzi sunt simbolizate prin c₁, c₂ ,, c_p. Ca exemple de astfel de comenzi se pot da: alegerea domeniului de masurare la aparate cu mai multe domenii, calibrarea interna, reglarea zeroului. Aceste operatii pot fi efectuate de catre operator sau pot fi efectuate automat de dispozitive construite in acest scop.

In cazul masurarii indirecte a unei marimi dependente de doua sau mai multe marimi, caracteristica statica de transfer ideala este exprimata cu o relatie de forma:

, (6)

unde x_1,, x_n sunt marimile care definesc marimea de masurat.

Daca functia f este liniara, caracteristica statica de transfer va fi reprezentata de un plan in spatiul n dimensional, iar daca f este neliniara, caracteristica statica va fi reprezentata de o suprafata curba.

In oricare caz, stabilirea finala a caracteristicii statice se face experimental prin operatia de etalonare si ea se recunoaste in scara sau in curbele de intrare iesire ale aparatului.

Sensibilitatea Pentru a evidentia modul in care marimile de influenta se manifesta asupra rezultatului masurarii in ipoteza ca aceste marimi au variatii relativ mici, se recurge la dezvoltarea in serie Taylor a relatiei (2) si la retinerea termenilor de prima aproximatie. Se obtine:

, (7)

in care termenii cu Dp si cei cu Di reprezinta eroarea de masurare datorata fiecarui factor de influenta.

Tabelul 1. Caracteristici de transfer reprezentative

pentru aparatele de masurare analogice

Derivatele de ordinul intai din relatia (7) au semnificatia unor sensibilitati si anume: f x reprezinta sensibilitatea utila a aparatului, pe cand celelalte derivate reprezinta sensibilitati parazite, care trebuie reduse cat se poate de mult. Cu cat sensibilitatea utila este mai mare iar sensibilitatile parazite vor fi mai mici, cu atat caracteristica statica reala a aparatului de masurare se apropie de caracteristica ideala a acestuia.

Ceea ce deranjeaza mai mult in procesul masurarii sunt variatiile marimilor de influenta p_1,, p_n si i_1,, i_m, si nu valorile lor absolute. Daca ele ar ramane constante ar putea fi evaluate si luate in considerare ca atare in expresia (2), ar putea fi compensate automat sau corectate de catre personalul de exploatare a aparatului de masurare.

In cazul unor factori de influenta variabili cu sensibilitati mari se impune introducerea unor dispozitive de compensare automata a efectului acestor factori, realizand astfel aparate de masurare cu efecte de influenta minime, incadrabile in limitele unor erori tolerate.

Sensibilitatea utila S a unui aparat de masurare este definita ca raportul dintre variatia marimii de iesire si variatia marimii de intrare ale aparatului respectiv, neglijind deci, influenta factorilor perturbatori si considerand ca y = f(x). Ea are semnificatia derivatei marimii de iesire a aparatului in raport cu marimea de masurat:

. (8)

Poate fi definita si o sensibilitate medie globala a aparatului de masurat sub forma:

(9)

in care intervine intreg domeniul de masurare D = x_max x_min

La aparate cu caracteristici statice liniare sensibilitatea este aceeasi pe intreg domeniul de masurare, pe cand la aparate cu caracteristici statice neliniare, aceasta este diferita pentru diverse valori ale marimii de intrare. In acest din urma caz putem defini o sensibilitate diferentiala sau locala, printr-o relatie de forma:

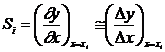, (10)

unde x_i cu i = 1, 2, , n reprezinta valori discrete ale lui x.

La aparate cu caracteristici neliniare nu se poate stabili o sensibilitate medie globala a intregului domeniu de masurare, dar se pot stabili sensibilitati medii pe subdomenii de masurare.

Dimensiunile sensibilitatii rezulta din dimensiunile marimii de iesire si ale marimii de intrare. Daca sensibilitatea are valori supraunitare se mai numeste si amplificare, iar daca are valori subunitare se mai numeste si atenuare.

Se poate defini si o sensibilitate relativa, adimensionala, exprimata de raportul dintre variatia relativa a marimii de iesire a aparatului si variatia relativa a marimii de intrare:

. (11)

Acest indicator este de preferat la compararea performantelor aparatelor de masurare cu domenii de masurare diferite.

La aparatele pentru masurari indirecte sensibilitatea se defineste in raport cu fiecare dintre marimile de intrare care definesc marimea de iesire.

In unele cazuri, in locul sensibilitatii se foloseste inversa acesteia, care este denumita constanta aparatului, adica

Constanta C a unui aparat reprezinta variatia marimii de masurat care produce o deviatie de o unitate sau de o diviziune pe scala aparatului.

Sensibilitatea unui aparat sau sistem de masurare este determinata de sensibilitatile elementelor componente ale acestuia si de modul in care acestea sunt interconectate. In cazul sistemelor cu caracteristici liniare, sensibilitatea ansamblului se poate deduce usor din sensibilitatile componentelor, dupa cum urmeaza.

Sensibilitatea unui sistem deschis cum este cel din figura 2 a, alcatuit din n elemente legate in serie, este egala cu produsul sensibilitatilor elementelor componente:

(13)

Acesta este cazul aparatelor cu convertire directa si al sistemelor deschise la care sensibilitatea sistemului este afectata de sensibilitatea fiecarui element component.

Sensibilitatea unui sistem inchis, cum este cel din figura 2,b, este definita de o relatie de forma:

, (14)

unde S₁ este sensibilitatea elementelor de pe legatura directa, iar S₂ este sensibilitatea elementelor de pe legatura inversa.

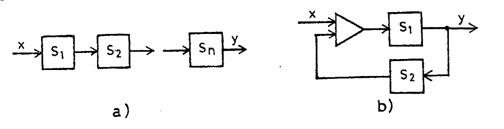
Fig.2. Referitor la calculul sensibilitatii.

a) sistem deschis; b) sistem inchis.

Daca S₁ >> S₂, atunci

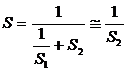(15)

prin urmare sensibilitatea intregului sistem este pratic determinata numai de sensibilitatea elementelor de pe legatura inversa.

1.2. Caracteristici de intrare

Cele mai importante caracteristici statice de intrare sunt: domeniul de masurare, pragul de sensibilitate si impedanta metrologica de intrare.

Domeniul de masurare. Acesta reprezinta intervalul D = x_max - x_min in care aparatul de masurare poate efectua o masurare corecta. El se situeaza pe caracteristica de transfer in zona care intereseaza pe utilizator si coincide cu gama de valori inscrise pe scala aparatului la aparate cu afisare analogica.

Valorile extreme ale domeniului de intrare x_min si respectiv de iesire y_min pot fi zero sau diferite de zero, de acelasi semn sau de semne diferite de semnul celeilalte valori extreme x_max, respectiv y_max. La unele aparate cu semnal unificat limita minima a valorii semnalului y este diferita de zero pentru x = 0.

Limitele domeniului de masurare sunt determinate de cerintele utilizatorului. Aplicarea la intrarea aparatului a unui semnal ce depaseste limita superioara, nu numai ca nu poate fi afisat, dar poate duce la defectarea aparatului utilizat.

La aparatele utilizate la masurari indirecte, limitele domeniului de masurare se deduc prin calcul din limitele corespunzatoare ale marimilor direct masurabile, conform relatiei prin care acestea definesc marimea ce se masoara indirect.

Sub aspectul domeniului de masurare, un aparat de masurare este cu atat mai bun cu cat domeniul de masurare al acestuia este mai mare, deoarece ofera posibilitati mai largi de utilizare. Pe de alta parte insa, extinderea domeniului de masurare in conditiile in care limitele fizice ale scalei raman aceleasi duce la dificultati in sesizarea variatiilor mici ale marimii de intrare prin dificultati de citire pe o scara foarte densa, precum si la complicarea aparatului de masurare.

Pentru eliminarea inconvenientelor de acest fel se recurge la folosirea de aparate de masurare cu mai multe scari, obtinute prin divizarea domeniului de masurare in doua sau mai multe subdomenii. Trecerea de la un subdomeniu la altul se face prin manevrarea unui comutator.

Pragul de sensibilitate. El este o caracteristica de intrare care defineste cea mai mica valoare a masurandului care determina o variatie certa, sesizabila, a marimii de iesire in conditii normale de masurare. Acest indicator este util indeosebi la masurari de precizie ale unor marimi de valori relativ mici.

Impedanta metrologica. In general conectarea oricarui element intr-un sistem de masurare, influenteaza atat elementele din amonte cat si pe cele din aval. Este de dorit, insa, ca influenta asupra elementului din amonte sa fie cat mai mica, iar influenta asupra elementului din aval sa fie cat mai puternica si bine definita.

Impedanta metrologica z_m defineste calitatea unui element dintr-un sistem de masurare de a nu influenta marimea de masurat, adica marimea din amonte, ci numai pe cea din aval. Valoarea acestui indice de calitate este legata de consumul de energie al elementului respectiv, mai precis, de energia consumata din cadrul obiectului masurarii. Cu cat impedanta metrologica este mai mare cu atat consumul de energie este mai mic si deci influenta asupra marimii de intrare este mai mica. Prin urmare, la alcatuirea unui sistem de masurare se pune problema alegerii unei impedante metrologice de intrare cat mai mare si a unei impedante metrologice de iesire cat mai mica.

1. Caracteristici de iesire

Principalele caracteristici de iesire sunt: forma de prezentare a rezultatului masurarii, rezolutia si precizia de masurare, exprimata prin clasele de precizie.

Forma de prezentare a rezultatului masurarii. Aceasta este dependenta de natura aparatului de masurare. Rezultatul masurarii poate fi prezentat in:

forma analogica;

forma numerica.

In primul caz este vorba de aparate de masurare de tip analogic la care rezultatul masurarii se prezinta prin pozitia unui indicator fata de scala aparatului sau printr-un grafic trasat de un inscriptor pe o hartie in miscare de deplasare liniara sau unghiulara. Discretizarea rezultatului masurarii, adica transpunerea rezultatului pe un numar o face utilizatorul aparatului de masurat prin 'citirea' rezultatului.

In al doilea caz este vorba de aparate de tip numeric sau de aparate de tip analogic dotate cu convertoare analog numerice la care rezultatul masurarii se prezinta direct sub forma numerica prin afisare cu ajutorul unor dispozitive cu LED-uri sau cu cristale lichide sau prin inregistrare (inscriere) numerica pe hartie la anumite intervale de timp.

Rezolutia. Aceasta este definita ca numarul de diviziuni elementare ale scalei, in cazul aparatelor cu afisare/inregistrare analogice, sau numarul maxim de cuante elementare corespunzator valorii maxime a masurandului, in cazul aparatelor cu afisare/inregistrare numerica. Astfel un AM care are scala gradata cu 200 diviziuni elementare are o rezolutie egala cu 200 sau egala cu 400 daca se iau in consideratie si jumatatile de diviziuni elementare. In general o diviziune reprezinta o unitate de masura sau o fractiune din aceasta.

Din cele aratate rezulta ca dintre doua aparate de masurare, care au acelasi domeniu de masurare, cel care are scala gradata in mai multe diviziuni are o rezolutie mai buna. O rezolutie mai buna se poate obtine prin extensia fizica a scalei sau prin marirea artificiala a acesteia cu ajutorul unei lupe.

In cazul aparatelor cu afisare/inregistrare numerica rezolutia este determinata de numarul de cifre semnificative cu care se face afisarea / inregistrarea. Astfel un aparat care afiseaza sau inregistreaza rezultatul masurarii cu patru cifre zecimale semnificative are o rezolutie egala cu 10 000, cea mai mica diferenta dintre doua valori consecutive pe care o poate sesiza aparatul fiind 1/10000, adica o cuanta de discretizare.

Precizia de masurare. Precizia de masurare a unui AM exprima calitatea lui de a furniza rezultate ale masurarii cat mai apropiate de valoarea reala a marimii masurate, deci cu erori de masurare cat mai mici. Prin urmare precizia se apreciaza dupa marimea erorii de masurare.

Eroarea admisibila maxima a unui AM este specificata pentru anumite conditii de efectuare a masurarilor si are doua componente distincte si anume:

eroarea admisibila normala numita si intriseca;

erori suplimentare.

Eroarea admisibila maxima normala este eroarea maxima cu care se fac masurari in conditii normale de lucru, numite si conditii de referinta care sunt precizate in norme sau standarde, in cazul aparatelor uzuale, ori sunt precizate in documentatia de folosire a aparatelor speciale. Este vorba de eroarea de masurare produsa de factorii de mediu (temperatura, umiditate, campuri electrice s.a.) in cazul cand acestia se incadreaza in limitele normelor sau standardelor si cand aparatul a fost montat corect si functioneaza, deci, in conditii normale. In aceste conditii efectele factorilor de influenta sunt reduse, de unde rezulta ca erorile admisibile de baza sunt in esenta erori sistematice si aleatoare tolerabile.

Erorile suplimentare sunt cele care apar atunci cand factorii de influenta ies din limitele considerate ca normale si care sunt specificate in norme sau documentatia AM. Ele se specifica pentru fiecare factor de influenta in parte si pe intervale de marimi ale acestora.

Erorile suplimentare sunt specifice fiecarui tip de AM si sunt cu atat mai mari cu cat conditiile de masurare se indeparteaza de conditiile normale si normate. De aceea ele sunt evaluate pe domenii de depasire, fie prin valori limita pe domenii, fie prin relatii de evaluare pe aceste domenii de depasire.

Erorile admisibile maxime pot fi exprimate sub forma de erori absolute, sub forma de erori relative sau sub o forma combinata. Relatia dintre eroarea absoluta Dx produsa de un AM si eroarea admisibila maxima sau tolerata, Dx_ma, a aparatului respectiv se prescrie prin inegalitatea:

(16)

In mod similar, relatia dintre eroarea relativa e si eroarea relativa maxima admisibila e_ma a AM este exprimata de inegalitatea:

(17)

Daca eroarea absoluta maxima este aceeasi in tot domeniul de masurare, eroarea relativa maxima este invers proportionala cu valoarea masurandului x, deci AM are eroarea relativa minima la valoarea maxima a masurandului. Daca insa eroarea absoluta maxima este proportionala cu valoarea masurandului, eroarea relativa maxima este constanta si anume:

, (18)

unde c este factorul de proportionalitate. Aceasta forma de exprimare a erorii relative (maxime) se foloseste in cazul contoarelor de energie, a frecventmetrelor s.a.

Eroarea normata maxima admisibila se prescrie, de asemenea, procentual prin raportarea erorii absolute maxime admisibile la o valoare conventionala x_c, astfel:

[%] . (19)

Ca valoare conventionala poate fi adoptata:

limita superioara a domeniului x_max daca x_min = 0;

diferenta limitelor domeniului adica x_max x_min

valoarea nominala a marimii masurate cand o astfel de recomandare este facuta.

Aceste forme de prescriere a erorii este recomandata pentru specificarea erorii maxime tolerate la aparate la care eroarea absoluta maxima se mentine aceeasi in tot domeniul de masurare. Este, deci, forma care se aplica la marea majoritate a AM intrucat permite compararea sub aspectul preciziei a aparatelor cu domenii de masurare diferite.

De remarcat faptul ca la aparatele care au o eroare absoluta constanta si au specificata eroarea normata maxima admisibila, eroarea relativa a acestora este invers proportionala cu valoarea marimii masurate:

Prin urmare pentru a avea erori relative mici se recomanda ca alegerea domeniului de masurare pentru o anumita aplicatie sa fie astfel facuta incat valorile curente ale marimii masurate sa se situeze aproape de limita superioara a domeniului de masurare, fara sa o depaseasca.

Daca un AM are o eroare absoluta maxima compusa dintr-o componenta constanta si dintr-o componenta proportionala cu marimea masurata, eroarea tolerata maxima se exprima sub forma unei erori relative combinate sub forma:

unde e_ma este componenta constanta a erorii relative provenita din eroarea absoluta, proportionala cu valoarea masurandului, iar al doilea termen reprezinta eroarea relativa, invers proportionala cu valoarea masurandului, care provine din eroarea relativa absoluta maxima constanta.

Evaluarea erorilor de masurare in cazul unor masurari efectuate in conditii diferite de cele normale necesita luarea in considerare a erorilor suplimentare, cauzate de factorii de influenta.

Clasele de precizie. Pentru unificarea exprimarii cantitative a preciziei de masurare orice aparat sau instalatie de masurare se incadreaza intr-o anumita clasa de precizie. Clasele de precizie (CP) sunt ierarhizate intr-o serie de trepte dupa valoarea maxima a erorii intriseci normate. Una dintre cele mai uzuale serii de trepte este urmatoarea: CP = 0,001; 0,002; 0,005; 0,01; 0,02; 0,05; 0,1; 0,2; 0,5; 1; 2; 5.

Un aparat incadrat intr-o anumita clasa de precizie are o eroare intrinseca maxima normata mai mica sau egala cu acea clasa de precizie. De exemplu, un aparat din clasa de precizie 0,1 are o eroare mai mica sau cel mult egala cu 0,1 din domeniul de masurare.

Clasele de precizie cu valori mici, exprimand erori tolerate mici, sunt clase de precizie inalta, pe cand cele cu valori medii si mari sunt clase de precizie medie si respectiv mica. Cunoscand clasa de precizie a unui aparat de masurare, care in mod normal trebuie sa fie inscrisa pe scala aparatului, se poate stabili valoarea maxima a erorii pe care o poate produce aparatul respectiv pe baza relatiei:

Eroarea relativa produsa la masurarea unei marimi x se determina din relatia:

(23)

Aplicatie. Cu un miliampermetru din clasa de precizie CP = 0,1 cu domeniu de masurare D = 2 - 10 mA, se masoara un curent de 8 mA. Sa se calculeze: eroarea absoluta maxima, eroarea relativa si intervalul de incadrare al valorii masurate.

- eroarea absoluta maxima:

- eroarea relativa pentru i = 8 mA:

- intervalul de incadrare

1.4. Caracteristici de constructie si de exploatare

Performantele unui aparat de masurare ca si ale altor elemente ale unui sistem sunt determinate atat de principiul metodei care sta la baza conceptiei aparatului respectiv, de modul cum acesta a fost realizat efectiv, cat si de conditiile de exploatare si de intretinere. Cei mai importanti indici de calitate privind realizarea fizica si exploatarea aparatelor sunt robustetea si fiabilitatea.

Robustetea. Prin robustete se intelege calitatea unui aparat de a functiona corect in conditii severe de exploatare. Despre un aparat se spune ca este cu atat mai robust cu cat acesta poate suporta actiuni mai intense ale unor factori externi cum ar fi: socurile, vibratiile, variatiile de temperatura si de presiune, umiditatea, precum si variatii bruste ale marimii de masurat.

Robustetea este legata si de capacitatea de supraincarcare in sensul ca un aparat sau sistem poate suporta valori ale marimii de masurat care depasesc limita superioara a domeniului de masurare fara a se defecta si fara sa-si modifice nici una dintre caracteristicile functionale: precizia, sensibilitatea, liniaritatea s.a.

Capacitatea de supraincarcare se exprima prin raportul dintre valoarea maxima nedistructiva a marimii de masurat si limita superioara a domeniului de masurare al aparatului. Aceasta se asociaza, de regula, cu un anumit interval de timp, intrucat efectele unei supraincarcari depind si de durata supraincarcarii. Astfel, putem defini o capacitate de supraincarcare pe timp scurt (soc) si o capacitate de supraincarcare pe timp determinat (suprasarcina).

Robustetea si capacitatea de supraincarcare prezinta interes deosebit in cazul aparaturii industriale care functioneaza in conditii grele si cu fluctuatii foarte mari. In consecinta pentru a imbunatati acesti indici se prevad inca din constructie masuri de protejare cum ar fi: alegerea adecvata a materialelor, acoperiri de protectie, etansari, suspensii elastice, compensari termice, ecranari magnetice si electrice, membrane de separatie.

Fiabilitatea metrologica. Prin fiabilitate metrologica se intelege proprietatea unui element sau sistem de masurare de a functiona in limitele parametrilor lui metrologici de proiectare, fara defectiuni, un timp cat mai indelungat.

Intervalul de timp in care un element sau sistem isi pastreaza capacitatea de functionare in limitele tolerantelor admise, cu pauzele necesare pentru intretinere si mici reparatii, constituie durata de functionare sau de viata a acestuia.

Putem distinge trei feluri de fiabilitate:

fiabilitatea apriorica, este cea care se determina prin calcule pe baza datelor teoretice privind elementele componente, interconectarea lor si conditiile de functionare;

fiabilitatea tehnica, este cea care se determina experimental pe standuri in intreprinderea producatoare;

fiabilitatea operationala sau reala, este cea care se determina in conditii reale de exploatare sub actiunea complexa a factorilor reali din diverse domenii.

Data fiind multitudinea factorilor ce trebuie luati in consideratie, evaluarea fiabilitatii constituie o problema complexa care necesita reliefarea mai multor aspecte.

In mod curent, ca masura a fiabilitatii se adopta probabilitatea functionarii fara defectiuni in decursul unui interval de timp t, in conditii date. Intervalul de timp T, in care un aparat functioneaza fara defectiuni, constituie o variabila aleatoare si este numita timp de functionare fara defectiuni. Acest timp T poate fi evaluat probabilistic cu relatia:

Prob

unde F(t) reprezinta probabilitatea de defectare in intervalul de timp T. Aceasta creste cu t si tinde catre 1 cand t . Probabilitatea ca aparatul sa functioneze corect, fara defectiuni in intervalul de timp T se obtine din relatia:

Prob

unde R(t) este functia de fiabilitate a aparatului respectiv (fig. 3). Aceasta scade cu t si tinde catre 0 cand t

Functia se poate determina experimental pe baza urmaririi comportarii unui numar N_a de aparate pe anumite intervale de timp. Daca intr-un prim interval de timp N_afd aparate nu au suferit defectiuni, valoarea estimata a functiei de fiabilitate este:

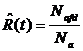. (26)

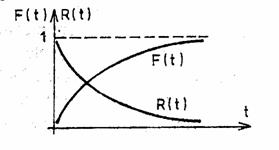
Fig. Functia de fiabilitate.

Repetand experimentul pentru valori ale lui t din ce in ce mai mari se obtin o serie de valori pentru care permite trasarea unei curbe ca cea din figura

Daca N_a este suficient de mare, valorile estimate ale lui tind catre cele reale iar, la limita, cand N_a se obtin chiar valorile lui R(t).

In evaluarea fiabilitatii mai pot fi folositi si alti indicatori cum sunt: frecventa de aparitie a defectelor f(t), media timpului de buna functionare T_m si intensitatea de aparitie a defectelor l(t)

Frecventa de aparitie a defectelorse poate estima experimental impartind numarul de defectiuni N_d care apar in intervalul de timp Dt la acel interval de timp si la numarul de aparate din lotul supus experimentului, adica:

. (27)

Pentru N_a si Dt 0, tinand seama de (24) si (25) se obtine frecventa reala de aparitie a defectelor sub forma:

(28)

De observat ca reprezinta densitatea de repartitie de probabilitate a timpului de buna functionare.

Media timpului de buna functionare T_m, pe o perioada de timp t, se poate obtine din f(t) prin integrare:

(29)

La limita, cand t si R(t) 0, integrand prin parti se obtine:

Intensitatea de aparitie a defectelor l(t), sau rata defectarilor, cum se mai numeste, se poate estima experimental impartind numarul de defecte N_d la intervalul de timp Dt in care s-au produs si la numarul N_af de aparate aflate in functiune la momentul t, adica:

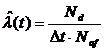(31)

Pentru N_a si Dt 0, se obtine expresia teoretica a ratei defectarilor sub forma:

care exprima densitatea de repartitie a defectarii la momentul t, considerand ca aparatul a functionat fara defectiuni pana la acel moment.

Pe baza datelor experimentale asupra unui mare numar de loturi si de aparate s-a constatat ca l evolueaza in timp asa cum se arata in figura 4, unde se disting trei perioade caracteristice:

perioada de tinerete (de rodaj) in cadrul careia apar defectiunile de fabricatie nedepistate de controlul tehnic uzinal;

perioada de functionare normala, cand rata defectarilor este relativ scazuta si constanta;

perioada de imbatranire sau uzura, cand rata defectiunilor este in crestere.

Cerinte ergonomice si estetice. In afara de indicatorii de calitate mentionati mai inainte, este necesar sa fie luate in considerare si aspectele privind ergonomia procesului de masurare si mai ales de citire a rezultatului masurarii, precum si aspectul estetic al aparaturii de masurare: formatul echipamentelor, dimensiunile, coloritul, iluminatul s.a.

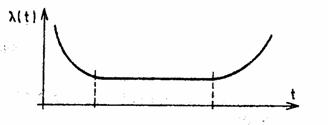
Fig.4. Intensitatea de aparitie a defectelor.

2. CARACTERISTICI DINAMICE

Masurarea unor marimi care variaza relativ rapid necesita printre altele si cunoasterea regimului dinamic al aparatului de masurare. Numai pe aceasta baza se poate face o alegere corespunzatoare a aparatului de masurare si se poate efectua o masurare corecta.

De remarcat ca variatiile rapide ale marimii de masurat nu pot fi sesizate imediat de unele aparate de masurare din cauza inertiei elementelor componente ale acestora. Inertia poate fi de natura mecanica, termica, electromagnetica.

In timpul regimurilor tranzitorii aparatele de masurare furnizeaza un rezultat eronat. De aceea este necesar ca preluarea rezultatului masurarii sa se faca dupa terminarea regimului tranzitoriu, adica dupa un interval de timp suficient de mare de la aparitia cauzei ultimului regim tranzitoriu.

Comportarea dinamica prezinta interes mai ales in cazul aparatelor pentru masurari dinamice rapide dar si in cazul traductoarelor si al altor elemente de automatizare care functioneaza in regim tranzitoriu. Cunoasterea regimurilor dinamice este importanta si in cazul aparatelor pentru masurari statice cu timp de raspuns mic ca si in cazul aparatelor pentru masurari multiple a mai multor marimi prin rotatie.

Problemele dinamicii sistemelor, inclusiv cele de masurare, sunt tratate exhaustiv in cadrul disciplinelor de automatica. In aceasta lucrare ne vom referi la o singura caracteristica dinamica si anume timpul de raspuns.

Timpul de raspuns al unui aparat sau sistem de masurare alcatuit din traductor si AM este definit ca intervalul de timp dintre momentul modificarii in salt a marimii de masurat pana in momentul in care aparatul afiseaza/inregistreaza corect rezultatul masurarii.

Sub aspect dinamic aproape totalitatea aparatelor de masurare ca si a celorlalte aparate din componenta unui sistem de masurare (traductor, elemente de convertire/adaptare s.a) se comporta ca elemente de ordinul I, II sau superior cu factor de transfer egal cu 1 (x_r = x_m).

Modelul matematic al unui element static de ordinul I este de forma:

, (33)

unde T este constanta de timp.

Functia de transfer a acestui element este de forma:

iar raspunsul indicial al unui astfel de element este de forma:

(35)

si este reprezentat in graficul din figura 5,a.

Daca marimea de intrare ar avea si o variatie sinusoidala suprapusa peste variatia de timp treapta, raspunsul aparatului la o astfel de intrare ar fi ca cel reprezentat in figura 5,b.

Din graficele raspunsului se observa ca marimea masurata x_m urmareste marimea reala x_r, iar in timpul regimului tranzitoriu diferenta dintre aceste marimi, care este mare la inceput, se diminueaza spre sfarsitul regimului tranzitoriu si tinde catre zero cand t , ramanand insa un mic decalaj in timp in cazul variatiei sinusoidale a lui x_r .

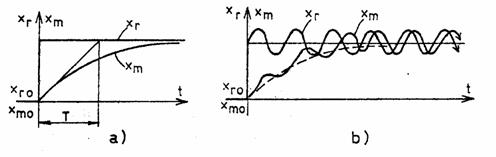
Fig. 5. Raspunsul elementului de ordinul I:

a) la variatia treapta; b) la variatia treapta si sinusoidala

O situatie asemanatoare o prezinta si elementele cu intarzieri de ordinul II. Modelul matematic al acestor elemente este de forma:

(36)

Functia de transfer este de forma:

, (37)

iar raspunsul indicial depinde de valorile constantelor de timp T_l si T₂.

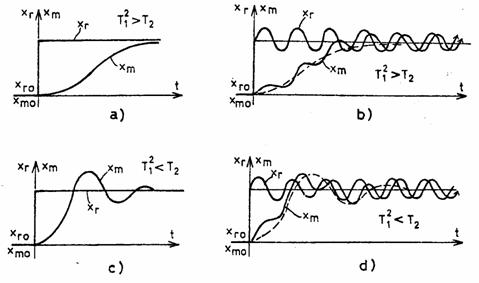
Fig. 6. Raspunsul elementului de ordinul II:

a), b) Element aperiodic la variatie treapta si la variatie treapta si sinusoidala;

c), d) Element oscilator la variatie treapta si la variatie treapta si sinusoidala.

Daca T₁² > 4T₂ procesul descris de model are un grad de atenuare mare iar tranzitia de la o stare la alta este aperiodica, asa cum se vede in figura 6,a, iar daca T₁² < 4T₂, procesul descris are un grad de atenuare mic, iar tranzitia de la o valoare a lui x_m la alta se face cu cateva oscilatii.

Din analiza graficelor prezentate in figurile 5 si 6 se constata o anumita asemanare intre curbele de raspuns, in sensul ca marimea x_m indicata de aparat urmareste cu o anumita intarziere marimea reala x_r si ca numai in regim stationar cele doua marimi se apropie cel mai mult una de cealalta. Decalajul si intarzierea sunt cu atat mai mari cu cat ordinul modelului matematic al aparatului sau sistemului de masurare este mai mare.

Din cele aratate rezulta ca valorile indicate de un aparat de masurat in timpul regimului tranzitoriu sunt eronate si ca preluarea valorilor marimii masurate trebuie sa se faca la sfarsitul regimului tranzitoriu. De aceea este foarte important sa se cunoasca timpul de raspuns al aparatelor de masurare utilizate.

Timpul de raspuns real este definit ca intervalul de timp din momentul modificarii marimii de intrare x_r pana in momentul cand marimea de iesire x_m atinge 95 - 98% din valoarea catre care tinde cand t . La elementele cu intarziere de ordinul I timpul de raspuns este de circa 4T, iar la cele de ordin superior este, evident, mai mare.

Aparatele cu cel mai mic timp de raspuns sunt aparatele optoelectronice, in speta osciloscoapele catodice care practic nu au inertie, timpul de raspuns fiind de ordinul fractiunilor de ms. si osciloscoapele optoelectromecanice au un timp de raspuns relativ mic, de ordinul catorva ms.

Aparatele de masurare electronice au timpul de raspuns relativ mic, de ordinul fractiunilor de secunda, pe cand aparatele de masurare de tip electromagnetic cu bobine mobile au timpul de raspuns de ordinul secundelor. Aparatele de masurare bazate pe efecte termice (schimb de caldura) au timp de raspuns de ordinul minutelor.

Numaratoarele universale au timpul de raspuns ce depinde de frecventa generatorului de impulsuri si de numarul de cifre cu care se face afisarea rezultatului masurarii.

Un timp de raspuns relativ mare au compensatoarele si puntile de masurare automate la care echilibrarea se face cu ajutorul servomotoarelor electrice reversibile de tip integrator. In aceste cazuri baleierea intregii scale se face in 1-5 secunde.

Dupa timpul de raspuns, aparatele de masurare sunt incadrate in urmatoarele categorii:

aparate pentru procese lente;

aparate pentru procese rapide.

Prin urmare, alegerea unui aparat de masurare pentru o aplicatie data trebuie facuta si dupa criteriul timpului de raspuns.

intrebari /Subiecte de control

Ce reprezinta caracteristicile statice ale unui aparat de masurare?

Ce reprezinta caracteristicile dinamice ale unui aparat de masurare?

Enumerati si comentati caracteristicile de transfer ale aparatelor de masurare.

Definiti si comentati notiunea de sensibilitate a aparatelor de masurare.

Definiti si comentati notiunea de impedanta metrologica.

Ce sunt si la ce servesc clasele de precizie?

Definiti notiunea de fiabilitate a unui aparat / sistem de masurare?

Definiti si comentati notiunea de robustete.

Definiti timpul de raspuns al unui aparat / sistem de masurare.