CALCULUL PROTECTIILOR CONTRA RADIATIILOR FOLOSIND METODA NUCLEELOR INTEGRALE PENTRU DIFERITE SURSE DE RADIATII

CALCULUL PROTECTIILOR CONTRA RADIATIILOR FOLOSIND METODA NUCLEELOR INTEGRALE PENTRU DIFERITE SURSE DE RADIATII

Pe langa alte metode existente, cea mai intens folosita este metoda nucleelor integrale care conduce in final la calculul integralelor pe volum sau pe suprafata. In aest sens au fost efectuate toate calculele pentru diferitele tipuri de surse punctuale, liniare, plane sau cilindrice.

Calculul protectiei trebuie sa porneasca de la ideea ca in spatele ecranului protector, doza primita de personalul expus sa nu depaseasca doza maxima stabilita de anumite norme si diferite grade de expunere conform recomandarilor CIPR (Comisia Internationala de Protectie contra Radiatiilor). Prin doza permisa se intelege doza ce permite o valoare acceptabila pentru individ si pentru populatie.

In continuare vom lua in considerare surse avand geometrii diferite. Lucram in ipoteza ca aceste surse de radiatii sunt izotrope, detectorul cu care inregistram intensitatea in punctele respective fiind de asemenea punctiform si izotrop; atenuarea este neglijabila si pentru simplitate, B = 1, B fiind factorul build up.

Sursa punctiforma

fara ecran

Intensitatea sursei S este:

rad/s

cu protectie concentrica

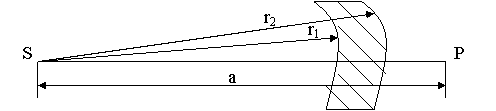
presupunem a >> r₂

unde

x = r₂ - r₁, x - grosimea zonei de protectie;

- coeficientul de absorbtie liniara.

Cu protectie plana

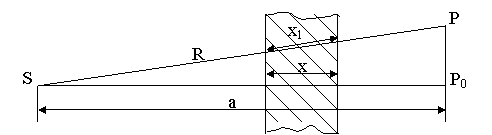
In acest caz, zona de protectie este o placa cu grosimea x si coeficient de absorbtie liniara .

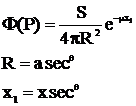
Sursa liniara

Fara ecran de protectie

Intensitatea sursei S_c este:

rad/cm sec

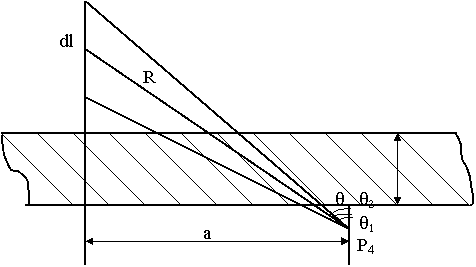
cu ecran de protecti

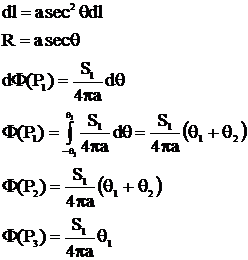
Zona de protectie are grosimea x;  fiind coeficientul de atenuare liniara.

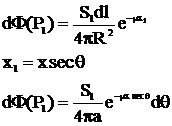
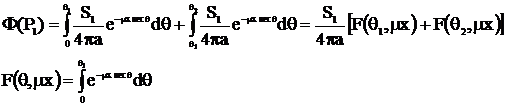
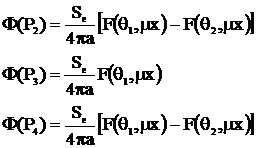
Sursa liniara

fara ecran de protectie

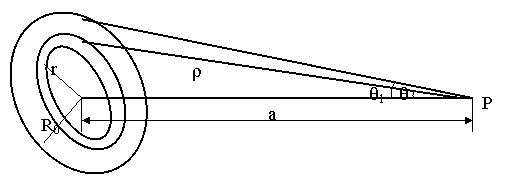
Intensitatea sursei S_a, radiatii / cm sec:

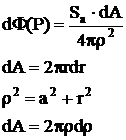
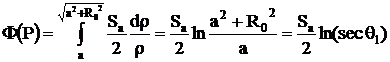
cu ecran de protectie

Zona de protectie are grosimea x, iar  este coeficientul de atenuare liniara.

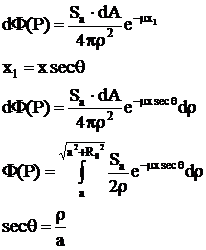
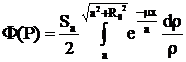
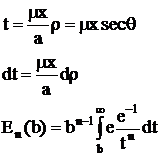
Sursa cilindrica

fara ecran de protectie

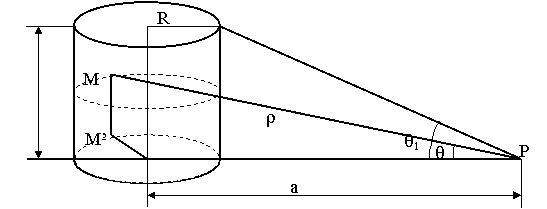
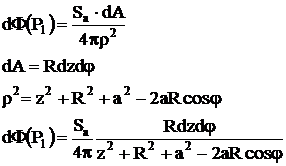
Se noteaza:

Inlcuind in relatia de mai sus se obtine:

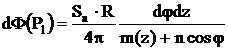
Integrand si prelcurand relatia rezulta:

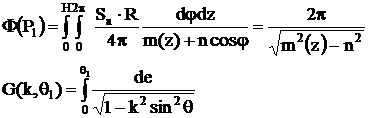
cu ecran de protectie

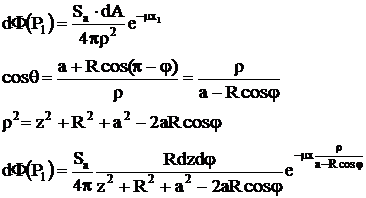
Se fac urmatoarele notatii:

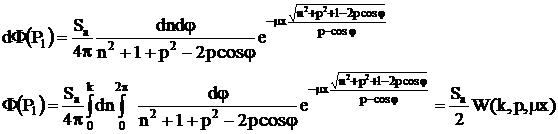
Avand mediul absorbant, fara ecran de protecte

Coeficientul de absorbtie liniara a mediului absorbant este ₀.

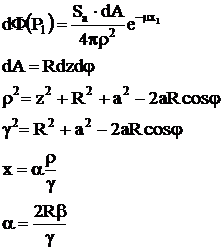
Se noteaza:

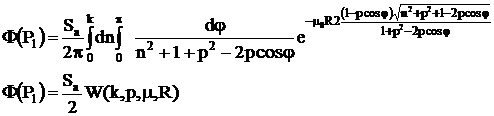
Cu ecran de protectie

Coeficientul de atenuare este , iar grosimea y.

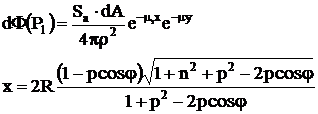
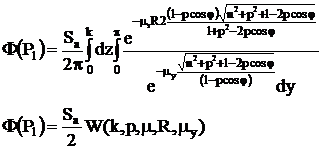
In toate aceste cazuri s-a luat in considerare fasciculele inguste de radiatii gamma , pentru B=1, coeficientul build up. In cazul fascisculelor largi, contributia radiatiilor imprastiate se ia in considerare pentru inceput, apoi coeficientul de absorbtie liniara si numarul atomic al mediului respectiv.

Relatia care da fluxul real este:

Deci, pentru a afla fluxul real vom inmultii factorul build-up cu fluxul determinat in cazul fasciculelor inguste. Evident nu este o simpla inmultire si de fapt operatia de ingustare pentru a afla fluxul total se efectueaza asupra acestui produs.

Vom avea

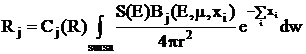
unde:

R_j - raspunsul detectorului de tip j;

C_j - coeficient de conversie;

S - sursa;

r - distanta sursa - detector;

B - factorul build-up;

dw - elementul de volum.

Aceasta relatie este valabila pentru radiatii monoenergetice. In cazul radiatiilor care eu energii diferite se integreaza si dupa E.

Factorul de acumulare build-up se exprima cu ajutorul seriei Taylor astfel:

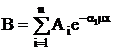
unde A_i, a sunt coeficienti independenti de grosimea protectiei, dar dependenti de energia si materialul protectiei.